Question
Question: The resistance per unit length of wire segment AB, BC, CD, DA is the same. The magnetic field due to...
The resistance per unit length of wire segment AB, BC, CD, DA is the same. The magnetic field due to current at point O is
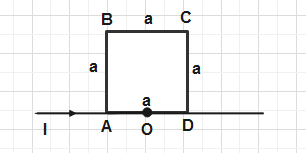
Solution
We have to apply here two concepts:- firstly the magnetic field at the end point so finite length of wire and secondly magnetic field at the middle point of finite length wire. Here we have to apply Biot Savart’s Law, that if a point lies on the wire then the magnetic field for that point is always zero.
Complete step-by-step solution:
For solving this question we have to apply the concept of magnetic field due to finite wire at the point which is at the one end of the wire as shown in this figure.
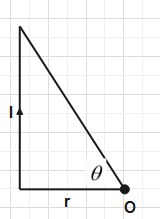
The magnitude of magnetic field at point O due to this finite length current carrying element is given by:
B=4πμ0rI(sinθ)
One more concept is applied in this question: magnetic field to finite length wire at a point which is the middle of wire as shown in the figure.
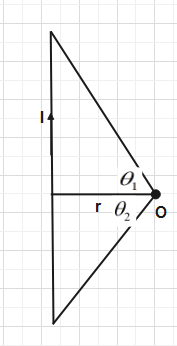
The magnitude of magnetic field at point O due to this finite length current carrying element is given by:
B=4πμ0rI(sinθ1+sinθ2)
Now the question is saying four segments AB, BC, CD, DA are having same resistance per unit length which means as their length is same so each wire is having the same value of resistance.
Let us assume the resistance of each wire is R.
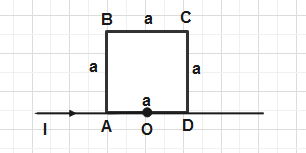
So, in this figure resistance of wire AD isR.
Since, Wires AB, BC, CD are in series so their net resistance is3R.
Since Single Wire AD and Combination of Wires AB, BC, CD are in parallel combination. So the potential difference between them is the same.
Let us current in branch AD =I1
Current in branch AB = I2
Since, Potential difference is same, so apply ohm’s law, we get
& {{I}_{1}}R={{I}_{2}}3R \\\ & \Rightarrow {{I}_{1}}=3{{I}_{2}} \\\ \end{aligned}$$ According to the figure. $$I={{I}_{1}}+{{I}_{2}}$$ $$\begin{aligned} & I=3{{I}_{2}}+{{I}_{2}} \\\ & \Rightarrow I=4{{I}_{2}} \\\ \end{aligned}$$ $$\therefore {{I}_{2}}=\dfrac{I}{4}$$ Put this value in above equation, we get , $${{I}_{1}}=\dfrac{3}{4}I$$. Now we calculate the magnetic field due to individual wires. So Magnetic field for wire AD is zero because point O lies on the wire. Magnetic field of AD is represented by$${{B}_{AD}}=0$$. Now we calculate the magnetic field from wire AB by using the above concepts. Let us assume the magnetic field for wire AB is represented by$${{B}_{AB}}$$. 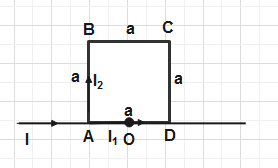 $${{B}_{AB}}=\dfrac{{{\mu }_{o}}}{4\pi }\dfrac{{{I}_{2}}}{AO}(Sin\theta )$$--- (Equation 1) Value of AO is half of AD. So, $$AO=\dfrac{a}{2}$$ and for calculating the value of sine angle we have to apply trigonometry relation, $$Sin\theta =\dfrac{AB}{BO}$$ Where, $$AB=a$$ OB is calculated by Pythagoras theorem. $$\begin{aligned} & O{{B}^{2}}={{a}^{2}}+{{(\dfrac{a}{2})}^{2}} \\\ & \Rightarrow OB=\dfrac{\sqrt{5}a}{2} \\\ \end{aligned}$$ Put this value in equation 1, we get $${{B}_{AB}}=\dfrac{{{\mu }_{o}}}{4\pi }\dfrac{\dfrac{I}{4}}{\dfrac{a}{2}}(\dfrac{2}{\sqrt{5}})$$ $$\Rightarrow {{B}_{AB}}=\dfrac{{{\mu }_{o}}}{4\pi }\dfrac{I}{2a}(\dfrac{2}{\sqrt{5}})$$ $$\therefore {{B}_{AB}}=\dfrac{{{\mu }_{o}}}{4\pi }\dfrac{I}{a\sqrt{5}}$$$$\otimes $$ Direction of this magnetic field is identified by the right hand thumb rule. So it comes inwards. Magnetic field due to wire CD is equal to wire AD and direction is also same so we can write , $$\therefore {{B}_{CD}}={{B}_{AB}}=\dfrac{{{\mu }_{o}}}{4\pi }\dfrac{I}{a\sqrt{5}}\otimes $$ Now we have to find magnetic field due to BC, Let us assume the magnetic field due to BC is represented as$${{B}_{BC}}$$. 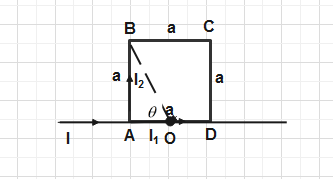 Using the above concept magnetic field due to wire BC at point O is represented as: $$\begin{aligned} & {{B}_{BC}}=\dfrac{{{\mu }_{0}}}{4\pi }\dfrac{I}{a}\left[ Sin(90-\theta )+Sin(90-\theta ) \right] \\\ & \Rightarrow {{B}_{BC}}=\dfrac{{{\mu }_{0}}}{4\pi }\dfrac{I}{a}\left[ Cos\theta +Cos\theta \right] \\\ & \Rightarrow {{B}_{BC}}=\dfrac{{{\mu }_{0}}}{4\pi }\dfrac{I}{a}(2Cos\theta ) \\\ \end{aligned}$$ Put the value of cosine from figure we , get $$\begin{aligned} & {{B}_{BC}}=\dfrac{{{\mu }_{0}}}{4\pi }\dfrac{I}{a}\times 2\times \dfrac{\dfrac{a}{2}}{\dfrac{\sqrt{5}a}{2}} \\\ & \therefore {{B}_{BC}}=\dfrac{{{\mu }_{0}}}{4\pi }\dfrac{I}{a}\dfrac{2}{\sqrt{5}}\otimes \\\ \end{aligned}$$ Since all the magnetic fields have the same direction, the net magnetic field is obtained by adding all the three magnetic fields and its direction is the same inwards. $${{B}_{net}}=({{B}_{AB}}+{{B}_{BC}}+{{B}_{CD}})\otimes $$ $$\begin{aligned} & \Rightarrow {{B}_{net}}=(\dfrac{{{\mu }_{o}}}{4\pi }\dfrac{I}{a\sqrt{5}}+\dfrac{{{\mu }_{o}}}{4\pi }\dfrac{2}{a\sqrt{5}}+\dfrac{{{\mu }_{o}}}{4\pi }\dfrac{I}{a\sqrt{5}})\otimes \\\ & \Rightarrow {{B}_{net}}=\dfrac{{{\mu }_{o}}}{4\pi }\dfrac{4I}{a\sqrt{5}} \\\ & \therefore {{B}_{net}}=\dfrac{{{\mu }_{o}}}{\pi }\dfrac{I}{a\sqrt{5}}\otimes \\\ \end{aligned}$$ This is the required answer of the question. **So the correct option is D.** **Note:** Here we have to apply the current login because in question resistance data is given and we know that current is series is same and in parallel it is different while in parallel potential difference is same. Here, Magnetic field at the point which lies on the axis of wire is always zero; this is proved by Biot Savart in its relation.