Question

The resistance of the coil of an ammeter is R. The shunt required to increase its range n-fold should have a resistance
$A.\dfrac{R}{n} \\\ B.\dfrac{R}{{n - 1}} \\\ C.\dfrac{R}{{n + 1}} \\\ D.nR \\\$

Answer 1

Shunt is the resistance which is connected across the resistance (R). If a high amount of current (greater than the rating of the ammeter) enters into an ammeter then, the coil of the ammeter will break. To improve the meter reading of the ammeter connected in line with the elements in the circuit, we need to insert a shunt resistance with the line resistance so that more amount of current can pass through the ammeter without breaking the coil.

Complete step by step answer:
Let us consider the shunt resistance connected across R be ${R_{sh}}$ and the initial rating of the ammeter is $I$ Amperes, and the resistance of the main coil in the ammeter is given as R. So, the voltage drop across R is ${V_R} = IR - - - - (i)$.

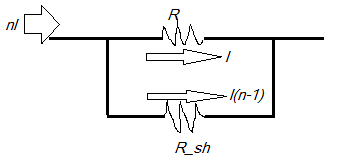
Now, according to the question, current increases to n-times, i.e., $I' = nI$ where the initial amount of current ($I$) will pass through the resistance R and the rest $nI - I = I(n - 1)$ will pass through the shunt resistance ${R_{sh}}$ , so the voltage drop across the shunt resistance is ${V_{{R_{sh}}}} = I\left( {n - 1} \right){R_{sh}} - - - - (ii)$

As discussed, the voltage drop across the parallel-connected resistance is equal. Therefore, by equation (i) and (ii), we can say that:

${V_R} = {V_{{R_{sh}}}} \\\ \Rightarrow IR = I(n - 1){R_{sh}} \\\ \Rightarrow {R_{sh}} = \dfrac{R}{{n - 1}} \\\$

Hence, the amount of the shunt resistance to increase the ammeter reading by n-fold is $\dfrac{R}{{n - 1}}$

So, the correct answer is “Option B”.

Note:
It is interesting to note here that the value of the shunt-resistance is always less than the main coil resistance so that the maximum amount of current will pass through it with less voltage drop. However, it is worth noting here that the voltage drop across the ammeter should remain constant which implies that the voltage drop in the parallel connected resistance should be the same.