Question

The resistance of the circuit between $A$ and $B$ is :

$\left( A \right)\;r$
$\left( B \right)\;0.5r$
$\left( C \right)\;2r$
$\left( D \right)\;3r$

Answer 1

The system seems to be much complicated, but it’s not. those vertical resistors can be eliminated in some ways and can reduce this circuit to a much simpler form. And just following series and parallel combination solving, we can solve this circuit much easily.

Complete step by step answer:
Let us consider we applied a potential V across points $A$ and $B$.
Now taking the upper part of this circuit

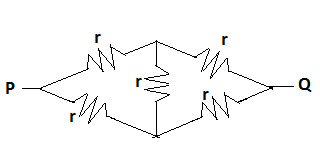
Here the point $P$ and $Q$ have the same potential.
Since all the resistor values are the same, this configuration holds the Wheatstone bridge condition.$\dfrac{P}{Q} = \dfrac{R}{S}$, here, $P = Q = R = S = r$
According to that condition, no current will flows through the vertical resistor.
In this similar manner, we can also consider the lower half of the circuit. Which also holds the Wheatstone bridge condition. So there also no current that will flow through the vertical resistor.
Since no current flows through those vertical resistors, there will be no potential drop across those resistors. So that, these resistors don’t contribute to the equivalent resistance of the circuit.
Now, we can redraw the circuit after eliminating those vertical resistors as,

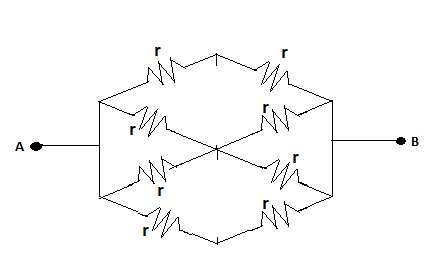
For simplicity, we can further redraw it as,

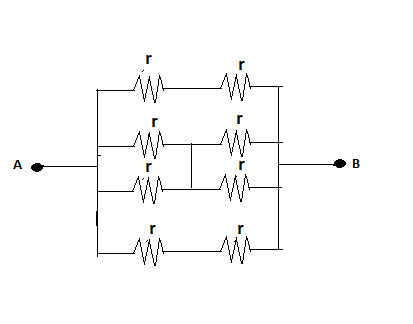
We know, how to find equivalent resistances in various cases.
If resistances are in series Just add them to get equivalent resistance ${R_{eq}} = {R_1} + {R_2}$
If resistances are in parallel, then $\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}$
By using these two relations we can further solve this circuit as,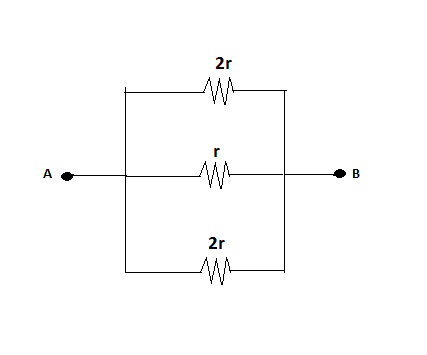
Now we can find out equivalent resistance between A and B easily
$\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{2r}} + \dfrac{1}{r} + \dfrac{1}{{2r}}$
$= \dfrac{4}{{2r}} = \dfrac{2}{r}$
Then, we get ${\operatorname{R} _{eq}} = \dfrac{r}{2}$
So the answer is option $\left( B \right) \Rightarrow 0.5r$.

Note:
We can approach this question differently as since there exists asymmetry between the vertical line, we can say that no current flows through those two vertical resistors. And without mentioning the Wheatstone bridge condition we can solve the problem.