Question

The resistance of an ammeter is $13\Omega$ and its scale is graduated for a current up to $100A$ . After an additional shunt has been connected to this ammeter, it becomes possible to measure currents up to $750A$ by this meter. The value of the shunt resistance is:
(A) $20\Omega$
(B) $2\Omega$
(C) $0.2\Omega$
(D) $2k\Omega$

Answer 1

Hint
The shunt resistance in any circuit is connected across the ammeter. So the potential drop across the shunt will be the same as that across the ammeter. So by equating the values of the potential drop we get $S = \dfrac{{{I_A}R}}{{\left( {I - {I_A}} \right)}}$
Formula used: To solve this problem, we use the following equations,
${\text{Potential drop}} = IR$
Where $I$ gives the current across the component
and $R$ gives the resistance of the component.

Complete step by step answer
To solve this problem we first need to draw the circuit.

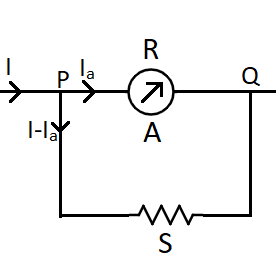
From the circuit, let us consider the resistance of the ammeter $R = 13\Omega$ . Now the current across the ammeter is given by, ${I_a} = 100A$ .
From the question, the total current in the circuit is $I = 750A$ .
So according to the circuit, the remaining current is passing through the shunt $S$ , given by $I - {I_a} = \left( {750 - 100} \right)A$
Now, since the ammeter and the shunt are connected across the same terminals PQ, so the potential drop is equal for them because, for parallel circuits across the same points, the potential drop remains the same.
Therefore from Ohm’s law potential drop across the ammeter is
$V = {I_a}R$
and the potential drop across the shunt is given by,
$V = \left( {I - {I_a}} \right)S$
Therefore, equating the above equations we get,
${I_a}R = \left( {I - {I_a}} \right)S$
Now, to find $S$ , we get by arranging the equation,
$S = \dfrac{{{I_a}R}}{{\left( {I - {I_a}} \right)}}$
Now by equating the values of the various components we get,
$S = \dfrac{{100 \times 13}}{{\left( {750 - 100} \right)}}$
By doing the calculation we get,
$S = \dfrac{{1300}}{{650}}$
Therefore, by dividing the values,
$S = 2$
So the value of shunt resistance has to be $2\Omega$.
So the correct answer is option (B).

Note
The ammeters have inbuilt resistance in them, but sometimes when there is a very high current in the circuit a shunt resistance is placed parallel to the ammeter so that the high current passing through the ammeter does not cause any damage to it. So the shunt resistance is always placed parallel to the ammeter.