Question

The resistance of a heater coil is $110\Omega$. A resistance R is connected in parallel with it and combination is joined in series with resistance of $11\Omega$ to a 220V main line. The heater operates with a power of 110W. The value of R in ohm is
A) 12.22
B) 24.42
C) Negative
D) That the given value is not correct

Answer 1

In the above question, it is described as to how the heater coil is connected in the circuit. It is given that the heater coil operates at 110W and hence we can obtain the potential difference across the coil knowing the resistance. Further since the R ohm resistor is connected in parallel with the heater coil, the potential difference across R will be the same. Hence knowing the current in the circuit from ohms law we will determine the resistance of R in ohms.

Complete step-by-step solution:
To begin with let us first draw the circuit diagram of the above described circuit.

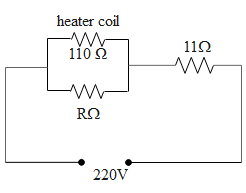
In the question it is given to us that the heater coil operates at a power of 110W. If P is the power of the heater with resistance R, then the potential difference ‘V’ across the heater coil is given by,
$\begin{aligned} & P=\dfrac{{{V}^{2}}}{R} \\\ & \because P=110W,\text{ }R=110\Omega \\\ & \Rightarrow 110W=\dfrac{{{V}^{2}}}{110\Omega } \\\ & \Rightarrow {{V}^{2}}={{\left( 110 \right)}^{2}} \\\ & \therefore V=110\text{V} \\\ \end{aligned}$
Two resistors connected in parallel have the same potential difference. Hence the potential difference across resistance R ohms is also 110V.
From the above circuit we can see that the main line of E = 220V is getting dropped across the combination of resistors ${{V}_{C}}$ i.e.( heater coil and R) and across 11ohm resistor ${{V}_{R}}$. Hence using Kirchhoff’s law in a closed circuit we obtain,
$\begin{aligned} & E={{V}_{C}}+{{V}_{R}} \\\ & \Rightarrow 220V=110V+{{V}_{R}} \\\ & \therefore {{V}_{R}}=110\text{V} \\\ \end{aligned}$
If the potential difference ‘V’ is applied across the a resistor of resistance ‘R’ , than from Ohm’s law the current ‘i’ in the circuit is given by,
$V=iR$
The resistance of 11 ohms is in series with the coil and the resistor R implying the current across them will be the same. Hence from ohms law the current ‘i’ in above the circuit is equal to,
$\begin{aligned} & {{V}_{R}}=iR \\\ & \Rightarrow 110V=i11\Omega \\\ & \therefore i=\dfrac{110V}{11\Omega }=10A \\\ \end{aligned}$
From ohms law the current across the heater coil is equal to,
$\begin{aligned} & {{V}_{C}}=iR \\\ & \Rightarrow 110V=i110\Omega \\\ & \therefore i=\dfrac{110V}{110\Omega }=1A \\\ \end{aligned}$
Since the current through the coil is 1A and the entering the junction of the coil and the R ohms resistor is 10A, from Kirchhoff’s junction rule the current across through the resistor of R ohms is 9A. Hence again using ohm's law the resistance of resistor R is,
$\begin{aligned} & {{V}_{C}}=iR \\\ & \Rightarrow 110V=9A\times R \\\ & \therefore R=\dfrac{110V}{9A}=12.22\Omega \\\ \end{aligned}$
Therefore the correct answer of the above question is option A.

Note: The Kirchhoff’s voltage law states that if we trace a closed loop in a circuit, the sum of the potential difference across the resistors in the circuit is equal to the sum of emf of the cell in the loop. If the path traced is in the direction of current then the potential difference across the resistors is taken as positive and the emf is taken as positive if we move across the cell from the negative to positive terminal of the cell. Similarly Kirchhoff’s junction rule states that the amount of current entering the junction is equal to that leaving the junction.