Question

The resistance between A and B is

& A)9\Omega \\\ & B)2\Omega \\\ & C)12\Omega \\\ & D)8\Omega \\\ \end{aligned}$$ $$E)20\Omega $$

Answer 1

In the given circuit diagram we have to first name all resistance then identify them which are in series and which are in parallel. The resistance in which flowing current is same are defined in series and in which current gets divided and potential difference across the terminals are same is defined in parallel combination.

Complete answer:
Name all resistance as $R_1$, $R_2$, $R_3$, $R_4$, $R_5$, $R_6$, $R_7$, $R_8$, $R_9$ are respectively as shown in a figure.

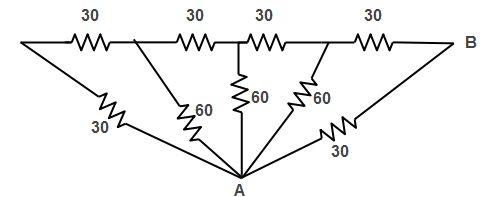
We will identify the resistance in series and parallel then we simplify them and obtain the effective resultant between A and B.
In the given Circuit firstly $R_1$ and $R_2$ are in series.
Let the resultant resistance of $R_1$ and $R_2$ is supposed to be $R_{s1}$.
So we apply the relation for series combinations of resistance.
${{R}_{s1}}={{R}_{1}}+{{R}_{2}}$
\Rightarrow $$$$\begin{aligned} & {{R}_{s1}}=30+30 \\\ & {{R}_{s1}}=60\Omega \\\ \end{aligned}
The effective value of $R_1$ and $R_2$ is$60\Omega$.
Now this $R_{s1}$ and $R_3$ are in parallel Combination.
Let the resultant resistance of $R_{s1}$ and $R_3$ is supposed to be $R_{p1}$
So we apply relation for parallel combination of resistance.
$\dfrac{1}{{{R}_{p1}}}=\dfrac{1}{{{R}_{s1}}}+\dfrac{1}{{{R}_{3}}}$
\Rightarrow $$$$\dfrac{1}{{{R}_{p1}}}=\dfrac{1}{60}+\dfrac{1}{60}
\therefore $$$${{R}_{p1}}=30\Omega
The effective value of $R_{s1}$ and $R_3$ is$30\Omega$.
Now $R_{p1}$ and $R_5$ are in series combination
Let the resultant resistance of $R_{p1}$ and $R_5$ is supposed to be $R_{s2}$
so we apply a relation for series combinations of resistance.
${{R}_{s2}}={{R}_{p1}}+{{R}_{5}}$.
\Rightarrow $$$${{R}_{s2}}=30+30
\therefore $$$${{R}_{s2}}=60\Omega
The effective value of $R_{p1}$ and $R_5$ is$60\Omega$.
Now this $R_{s2}$ is in parallel combination with $R_4$
Let their resultant is supposed to be $R_{p2}$.
$\dfrac{1}{{{R}_{p2}}}=\dfrac{1}{{{R}_{s2}}}+\dfrac{1}{{{R}_{4}}}$
\Rightarrow $$$$\dfrac{1}{{{R}_{p2}}}=\dfrac{1}{60}+\dfrac{1}{60}
\therefore $$$${{R}_{p2}}=30\Omega
Now this resistance $R_{p2}$ is series with $R_7$ and
Let their net resultant is supposed to be $R_{s3}$.
${{R}_{s3}}={{R}_{p2}}+{{R}_{7}}$
\Rightarrow $$$${{R}_{s3}}=30+30
\therefore $$$${{R}_{s3}}=60\Omega
Now this resistance $R_{s3}$ is parallel with $R_6$ and their resultant is represented by $R_{p3}$.
$\dfrac{1}{{{R}_{p3}}}=\dfrac{1}{{{R}_{s3}}}+\dfrac{1}{{{R}_{6}}}$
\Rightarrow $$$$\dfrac{1}{{{R}_{p3}}}=\dfrac{1}{60}+\dfrac{1}{60}
\therefore $$$${{R}_{p3}}=30\Omega
Now $R_{p3}$ and $R_8$ are in series and their resultant is represented by${{R}_{s4}}$.
\Rightarrow $$$$\begin{aligned} & {{R}_{s4}}={{R}_{p3}}+{{R}_{8}} \\\ & {{R}_{s4}}=30+30 \\\ & {{R}_{s4}}=60\Omega \\\ \end{aligned}
Now ${{R}_{s4}}$ and $R_9$ are in parallel combination and resultant is represented by $R_{AB}$.
$\dfrac{1}{{{R}_{AB}}}=\dfrac{1}{{{R}_{s4}}}+\dfrac{1}{{{R}_{9}}}$
\Rightarrow $$$$\dfrac{1}{{{R}_{AB}}}=\dfrac{1}{60}+\dfrac{1}{30}
\Rightarrow $$$$\dfrac{1}{{{R}_{AB}}}=\dfrac{1+2}{60}
\Rightarrow $$$$\dfrac{1}{{{R}_{AB}}}=\dfrac{3}{60}
\therefore $$$${{R}_{AB}}=20\Omega
So effective resistance between A& B is $20\Omega$.

So the correct option is E.

Note:
Current is measured in any circuit using an ammeter which is always connected in series in circuit while voltmeter is used in any circuit for measuring the potential difference which is always connected in parallel but these appliances do not measure the exact value because they are not ideal in nature.