Question

The remainder when $3^{37}$ is divided by 80 is

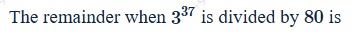
Answer 1

3

Answer 2

To find the remainder when $3^{37}$ is divided by 80, we use modular arithmetic.

We find that $3^4 = 81$, and $81 \equiv 1 \pmod{80}$.

We write the exponent $37 = 4 \times 9 + 1$.

So, $3^{37} = 3^{4 \times 9 + 1} = (3^4)^9 \times 3^1$.

Using the property of modular arithmetic, since $3^4 \equiv 1 \pmod{80}$, we have $(3^4)^9 \equiv 1^9 \equiv 1 \pmod{80}$.

Then, $3^{37} = (3^4)^9 \times 3^1 \equiv 1 \times 3 \pmod{80}$.

$3^{37} \equiv 3 \pmod{80}$.

The remainder is 3.