Question

The remainder when ${{27}^{40}}$ is divide by 12 is
(a) 3
(b) 7
(c) 9
(d) 11

Answer 1

Hint: First, we have to simplify ${{27}^{40}}$ in the reduced form that we will get as ${{\left( {{3}^{3}} \right)}^{40}}$ . Then we have to use the concept of binomial expansion using the formula ${{\left( a+b \right)}^{n}}=\sum\limits_{r=0}^{n}{{{\left( a \right)}^{n-r}}{{\left( b \right)}^{r}}}\times {}^{n}{{C}_{r}}$ . So, for a and b we can write 3 in the form of $\left( 4-1 \right)$ . And at last on solving the expansion, we will have the final answer in the form of $dividend=divisor\cdot quotient+remainder$ . Thus, we will get our required answer.

Complete step-by-step answer:
Here, we can write a simplified form of ${{27}^{40}}$ i.e. $27=3\times 3\times 3={{3}^{3}}$ . So, we can write ${{27}^{40}}={{\left( {{3}^{3}} \right)}^{40}}={{3}^{120}}$ .
Now, we can write ${{3}^{120}}$ as $3\times {{3}^{119}}$ . Also, we can simplify ${{3}^{119}}$ in the form of binomial expansion form i.e. ${{\left( 4-1 \right)}^{119}}$ . So, we will expand this using binomial expansion given as ${{\left( a+b \right)}^{n}}=\sum\limits_{r=0}^{n}{{{\left( a \right)}^{n-r}}{{\left( b \right)}^{r}}}\times {}^{n}{{C}_{r}}$ .
We will use this expansion and taking $a=4,b=-1,n=119$ we can write it as
${{\left( 4-1 \right)}^{119}}=\sum\limits_{r=0}^{119}{{{\left( 4 \right)}^{119-r}}{{\left( -1 \right)}^{r}}}\times {}^{119}{{C}_{r}}$
On expanding this expression, we get
$\begin{aligned} & ={{\left( 4 \right)}^{119}}{{\left( -1 \right)}^{0}}\times {}^{119}{{C}_{0}}+{{\left( 4 \right)}^{118}}{{\left( -1 \right)}^{1}}\times {}^{119}{{C}_{1}}+ \\\ & {{\left( 4 \right)}^{117}}{{\left( -1 \right)}^{2}}\times {}^{119}{{C}_{2}}+.....+{{\left( 4 \right)}^{1}}{{\left( -1 \right)}^{118}}\times {}^{119}{{C}_{118}}+ \\\ & {{\left( 4 \right)}^{0}}{{\left( -1 \right)}^{119}}\times {}^{119}{{C}_{119}} \\\ \end{aligned}$
On simplifying terms, we get
$={{\left( 4 \right)}^{119}}\times {}^{119}{{C}_{0}}-{{\left( 4 \right)}^{118}}\times {}^{119}{{C}_{1}}+{{\left( 4 \right)}^{117}}\times {}^{119}{{C}_{2}}+.....+\left( 4 \right)\times {}^{119}{{C}_{118}}-1$
(using ${}^{n}{{C}_{n}}=1$ )
Now, from above equation taking 4 common from expansion, we get
$=4\left( {{\left( 4 \right)}^{118}}\times {}^{119}{{C}_{0}}-{{\left( 4 \right)}^{117}}\times {}^{119}{{C}_{1}}+{{\left( 4 \right)}^{116}}\times {}^{119}{{C}_{2}}+.....+{}^{119}{{C}_{118}} \right)-1$
We know that on solving the bracket terms, we will get integer value so, we will assume that whole bracket as constant term let say c. So, we will get
${{\left( 4 \right)}^{118}}\times {}^{119}{{C}_{0}}-{{\left( 4 \right)}^{117}}\times {}^{119}{{C}_{1}}+{{\left( 4 \right)}^{116}}\times {}^{119}{{C}_{2}}+.....+{}^{119}{{C}_{118}}=c$
${{\left( 4-1 \right)}^{119}}={{3}^{119}}=4\left( c \right)-1$ ………………………(1)
So, substituting this value of equation (1) in ${{3}^{120}}=3\times {{3}^{119}}$ we get
${{3}^{120}}=3\times {{3}^{119}}=3\times \left( 4\left( c \right)-1 \right)$
On multiplying the brackets, we get
${{3}^{120}}=12c-3$
Now, we have to split $-3$ as $-3=-12+9$ . So, on putting this value, we get
${{3}^{120}}=12c-12+9$
Taking 12 common from first two terms, we get
${{3}^{120}}=12\left( c-1 \right)+9$
So, this is in the form of $dividend=divisor\cdot quotient+remainder$
Thus, we have remainder 9 when ${{27}^{40}}$ is divided by 12.
Hence, option (c) is correct.

Note: Another approach and simple way to find remainder is taking odd and even power of 3 and dividing it by 12 and checking the remainder. So, if we take ${{\left( {{3}^{3}} \right)}^{40}}$ then dividing 27 by 12, we get remainder as 3.

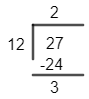
And when we take even power i.e. ${{3}^{4}}=81$ on dividing it by 12 we get remainder as 9.

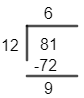
So, here we have ${{27}^{40}}={{3}^{120}}$ so 120 is even power hence the remainder will be 9 when divided by 12.