Question

The relation between $V_1$,$V_2$ and $V_3$ is:

Answer 1

We know that tension is the action-reaction pair force which is acting on the cables here. And it is the opposite of compression. To solve this question, we can begin by drawing the free body diagram of the multi-pulley system and the forces acting on it and then find its tension.

Complete step-by-step answer:
We know that a pulley is a simple device will can lift heavy objects with minimum energy. Here a block of some mass is attached to the pulley. A pulley consists of a tensile string or rope, which is used to tie and lift the heavy body and a shaft above which the string is kept. The shaft is circular generally and allows the easy movement of the string.
The force needed to lift the massive body is greater than the force needed to pull it using a pulley. Hence pulleys are used to lift heavy objects
Tension is a constant force which acts on the connecting medium like a rope or cable as discussed here. This is majorly a pulling force which tries to maintain the net force acting on the object. It is generally given as the product of mass of the given object and the sum of the acceleration and gravitational force acting on the body at any given time. i.e. mathematically expressed as T-mg = ma
It arises due to Newton's third law, that every action which is the gravitational force acting on the lift has an equal and the opposite reaction, which is the tension of the cable and the force due to upward acceleration.
Consider the free body diagram as shown below:

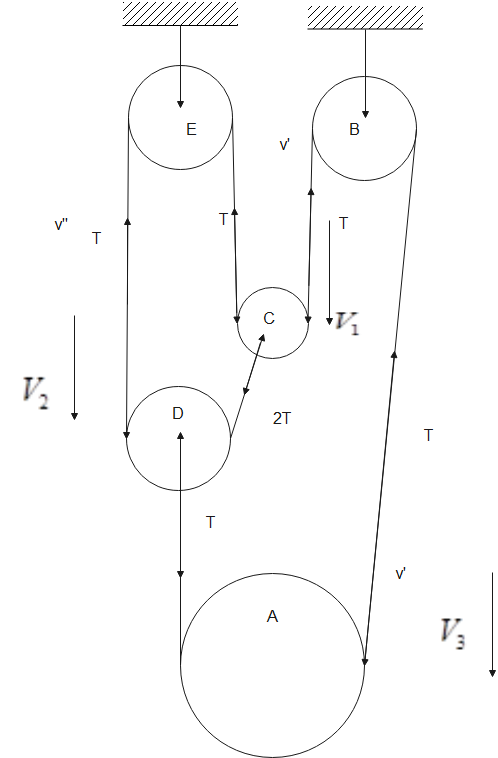
Since tension remains the same in any rope and considering the forces on A, B,C we have in pulley A
$-v_3=\dfrac{v\prime -v_2}{2}$
In pulley B
$-v_1=\dfrac{v\prime -v\prime \prime}{2}$
In pulley C
$-v_2=\dfrac{v\prime \prime-v_1}{2}$

Note: The tension on the cable is a non-negative physical quantity acting in the one dimension. If there is no kinks in the cable or its similar material which holds a heavy object, then the tension is equal to the magnitude of the force acting on the other end of the cables.