Question

The relation between the polarizing angle and the critical angle is
$\left( a \right)\,\,{i_p} = {\tan ^{ - 1}}\left( {{\text{cosec}}\,{\theta _c}} \right)$
$\left( b \right)\,\,{i_p} = {\tan ^{ - 1}}\left( {\sin \,{\theta _c}} \right)$
$\left( c \right)\,\,{i_p} = {\cot ^{ - 1}}\left( {\sin \,{\theta _c}} \right)$
$\left( d \right)\,\,{i_p} = {\cot ^{ - 1}}\left( {{\text{cosec}}\,{\theta _c}} \right)$

Answer 1

Critical angle is the angle of incidence for which angle of refraction is ${90^ \circ }$. The angle of incidence at which the reflected light is completely plane polarized is called polarizing angle or Brewster’s angle.
Formula used:
Relation between Refractive Index and Critical Angle:
$\mu = \dfrac{1}{{\sin c}}$ Here, c is the critical angle.

Complete Step by Step Answer:
The critical angle is the angle of incidence for which angle of refraction is ${90^ \circ }$.
Total internal reflection is the phenomenon that involves the reflection of all incident light off the boundary. It only takes place when following conditions are met;
$i)$Light should travel from denser medium to rarer medium.
$ii)$Angle of incidence is a denser medium should be greater than the critical angle for a pair of media in contact.

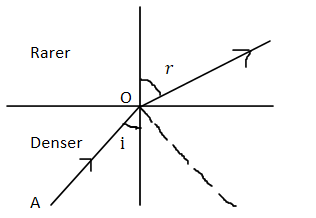
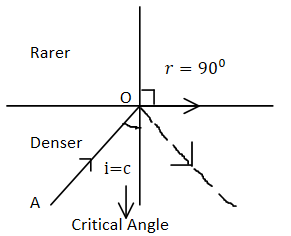
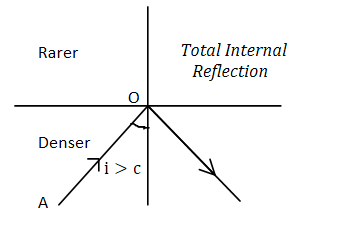
The angle of incidence at which the reflected light is completely plane polarized is called polarizing angle or Brewster’s angle.
If the electric field vectors are restricted to a single plane by filtration of beam with specialized materials, then light is referred to as plane or linearly polarized.
All waves vibrating in a single plane are called plane polarized.
Now, according to the question we need to find a relation between critical angle and polarizing angle. $\Rightarrow \mu = \dfrac{1}{{\sin c}}$ , and we will name it equation $\left( 1 \right)$
Also we have
$\mu = \tan {i_p}$ , and we will name it equation $\left( 2 \right)$
On equating equation $\left( 1 \right)$ and $\left( 2 \right)$ , we get
$\Rightarrow \dfrac{1}{{\sin c}} = \tan {i_p}$
And it can also be written as
$\Rightarrow {\text{cosec}}\,\,c = \tan {i_p}$ , as we know $sin\theta = \dfrac{1}{{{\text{cosec}}\,\,c}}$
And therefore, ${i_p}$ will be equal to
$\Rightarrow {i_p} = {\tan ^{ - 1}}\left( {{\text{cosec}}\,\,c} \right)$

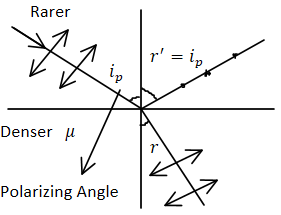
Hence, option $\left( a \right)$ is correct.

Note: The reflected light contains vibrations of an electric vector perpendicular to the plane of incidence. All waves vibrating in a single plane are called plane polarized. Hence, the reflected light is completely plane polarized in a direction perpendicular to plane of incidence.