Question

The relation between T and g is given by
$\begin{aligned} & \text{A}\text{.}T\propto g \\\ & \text{B}.T\propto {{g}^{2}} \\\ & \text{C}.{{T}^{2}}\propto g \\\ & \text{D}.T\propto \sqrt{\dfrac{l}{g}} \\\ \end{aligned}$

Answer 1

In the question we are asked to find the relation between ‘T’ and ‘g’. Consider a mass “m” suspended on a wire of length ‘$l$ ’ undergoes simple harmonic motion, ‘T’ is the time period, the time required to complete one oscillation and ‘g’ is the acceleration due to gravity (9.8m/s). To solve this we know the equation of time period; by squaring the known equation we can formulate the relation between ‘T’ and ‘g’.

Formula used:
$T=2\pi \sqrt{\dfrac{l}{g}}$
Time period of a simple oscillation is given by

Complete answer:
To find the relation between ‘T’ and ‘g’,
Let us consider ‘$l$ ’ to be the length of the pendulum.
As we know, time period is given by the equation
$T=2\pi \sqrt{\dfrac{l}{g}}$
Squaring both sides of the equation, we get
${{T}^{2}}=4{{\pi }^{2}}\dfrac{l}{g}$
From this equation we get,
${{T}^{2}}\propto \dfrac{l}{g}$
Thus we can conclude that, $T\propto \sqrt{\dfrac{l}{g}}$, when l is unchanged.

So, the correct answer is “Option D”.

Additional Information:
Time of a simple pendulum derivation:

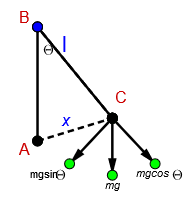
Consider a simple pendulum with a mass ‘m’ suspended on a wire of length ‘$l$ ’.
For one oscillation the pendulum is displaced at an angle of ‘$\theta$’ by ‘x’ distance.
Let ${{T}_{0}}$ be the time period at equilibrium.
${{T}_{0}}=mg$
When the pendulum oscillates, it is displaced at a small angle $\theta$
For this small displacement $\theta$, the restoring force acting will be
Restoring force=$-mg\sin \theta$
Since the angle of displacement $\theta$ is very small here, we can approximate $\sin \theta$ to $\theta$
I.e. $\sin \theta \approx \theta$
Hence the force here can be rewritten as
$F=-mg\theta$
Now let us consider the triangle ABC in the figure.
We know that sin of the angle $\theta$ is the ratio of the opposite side to the hypotenuse of the triangle. Since here $\sin \theta \approx \theta$, we can write this as
$\theta =\dfrac{opposite}{hypotenuse}$
Here the opposite side of the angle is the displacement ‘x’ and the hypotenuse of the triangle is length ‘$l$ ’ of the pendulum. Hence we can rewrite the equation as
$\theta =\dfrac{x}{l}$
Therefore the restoring force on the pendulum is
$F=-mg\theta =-mg\times \dfrac{x}{l}$
By Newton’s second law of motion, we have the equation of motion as
$F=ma$, Where ‘m’ is the mass of the body and ‘a’ is the acceleration.
We can rewrite this equation as
$a=\dfrac{F}{m}$
From the previous equation, we know that $F=-mg\dfrac{x}{l}$. Substituting this here, we get
$a=\dfrac{-mg\left( \dfrac{x}{l} \right)}{m}$
Eliminating the common terms, we get
$a=-\dfrac{g}{l}\times x$
For a simple harmonic motion we know that, $a=-{{\omega }^{2}}x$
On comparing both these equations, we get
$-{{\omega }^{2}}x=-\dfrac{g}{l}x$
By simplifying this,
${{\omega }^{2}}=\dfrac{g}{l}$
$\omega =\sqrt{\dfrac{g}{l}}$
Time period ‘T’ is given by the equation
$T=\dfrac{2\pi }{\omega }$
Substitute the value of $\omega$ in this equation
Therefore time period, $T=2\pi \sqrt{\dfrac{l}{g}}$

Note:
This question can be solved by another method.
We know that, for a simple pendulum its angular frequency $\omega$ is given by
$\omega =\sqrt{\dfrac{g}{l}}$
Time period of an oscillation can also be written as
$T=\dfrac{2\pi }{\omega }$
By substituting the value of angular frequency ($\omega$ ) in the above equation, we get
$T=2\pi \sqrt{\dfrac{l}{g}}$
Thus we get $T\propto \sqrt{\dfrac{l}{g}}$
Hence we get the same solution.