Question

The relation between magnetic field and current is given by Biot-Savart law. Illustrate Biot-Savart law with necessary figures.

Answer 1

Hint
The Biot-Savart law states that a small current-carrying conductor of length $dl$ and carrying a current $I$ is an elementary source of the magnetic field. Therefore this law can be used to calculate the magnetic field of certain distributions.

Complete step by step answer
The Biot-Savart law gives us the magnetic field that is associated with a current-carrying conductor. According to this law, the magnetic field at any point due to a current element $Idl$ is given by,
$\Rightarrow d\vec B = \dfrac{{{\mu _o}}}{{4\pi }}\dfrac{{Id\vec l \times \vec R}}{{{R^3}}}$
$\vec R$ is the distance of the current-carrying conductor from the point of observation and ${\mu _o}$ is the permeability of free space which has a value of ${\mu _o} = 4\pi \times {10^{ - 7}}N/{A^2}$ .
To derive this mathematical expression we consider a wire carrying current $I$ in a specific direction as in the figure,

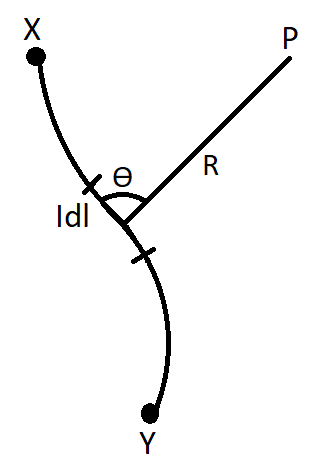
Let us consider a small element of wire $dl$ . The direction of this element is along the direction of the current in the wire. Now by using the Biot-Savart law we can calculate the magnetic field at the point P due to this current element.
The magnetic field at point P due to the element $dl$ is found to be proportional to the current in the wire, and the length of $dl$ and is inversely proportional to the square of the distance $R$ .
So we can write,
$\Rightarrow d\vec B \propto \dfrac{{Id\vec l \times \vec R}}{{{R^3}}}$
and removing the proportionality we get,
$\Rightarrow d\vec B = \dfrac{{{\mu _o}}}{{4\pi }}\dfrac{{Id\vec l \times \vec R}}{{{R^3}}}$
The magnitude of this field is given by,
$\Rightarrow \left| {d\vec B} \right| = \dfrac{{{\mu _o}}}{{4\pi }}\dfrac{{Idl\sin \theta }}{{{R^2}}}$.

Note
The Biot-Savart law is similar to Coulomb's law in a way as both of them are inversely proportional to the square of the distance between the source and the point. Using the Biot-Savart law we can calculate the magnetic fields of various current-carrying elements.