Question

The relation between edge length (a) and radius of atom (r) for BCC lattice is $\sqrt{3}a=4R$.
a. True
b. False

Answer 1

Use the property of a cube and calculate its diagonal. Then, relate this to the radius of atoms, present in the body-centred cubic cell. Assume that the radius of all atoms is the same.

Complete step by step answer:
In the classes of chemistry, we have studied the crystal lattices and also their edge length and relating parameters.
Let us first see the derivation of the diagonal of a cube and then see the relation of body centred cubic.
The structure for BCC is given as –

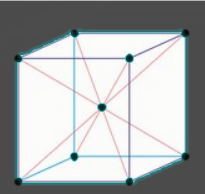
As we can see, in body centred cubic, there are 8 atoms at the corners of the cube. Each atom at the corner of the cube is shared by 8 unit cells. Therefore, the contribution per atom = 1/8.
Also, there is one atom at the centre of the unit cell (or cube).
Therefore, total atom per BCC unit cell = $\left( 8\times \dfrac{1}{8} \right)+1=2$
The body diagonal is defined as the direction from a corner of the cube to the farthest corner and this can be denoted by ‘bd’.
Now, face diagonal denoted by ‘fd’ can be related to body diagonal ‘bd’ by the Pythagoras theorem as,
$b{{d}^{2}}=f{{d}^{2}}+{{a}^{2}}$
where a is the length of cell edge.
$\Rightarrow b{{d}^{2}}={{a}^{2}}+{{a}^{2}}+{{a}^{2}}=3{{a}^{2}}$
Thus, the body diagonal is related to the cell edge by simplifying the above formula as,
$bd=\sqrt{3}a$
Now, one diagonal in a BCC contains a total radius of 2R, as seen in the below diagram.

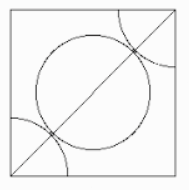
As we can see in the above diagram, the radius can be calculated as $R+2R+R=4R$
Therefore, equating both, we get $\sqrt{3}a=4R$

Therefore, the given statement is true.

Additional Information: The given structure is known as Body centred cubic unit cell (BCC) because there is an atom at the centre of the cubic body.

Note: A unit cell is the simplest unit of a complete crystal lattice and it is the most uniform unit, which is helpful in the analysis of the structure. There are four types of unit cell –
1. Simple or primitive unit cell
2. Body centred cubic unit cell (BCC)
3. Face centred cubic unit cell (FCC)
4. End centred cubic unit cell.