Question

The region between y=0 and y=d contains a magnetic field $\vec B = B\hat z$. A particle of mass m and charge q enters the region with a velocity $\vec v = v\hat i$. If $d = \dfrac{{mv}}{{2qB}}$, the acceleration of the charged particle at the point of its emergence at the other side is?
A. $\dfrac{{qvB}}{m}\left( {\dfrac{{\hat i + \hat j}}{{\sqrt 2 }}} \right)$
B. $\dfrac{{qvB}}{m}\left( {\dfrac{1}{2}\hat i - \dfrac{{\sqrt 3 }}{{\sqrt 2 }}\hat j} \right)$
C. $\dfrac{{qvB}}{m}\left( {\dfrac{{ - \hat j + \hat i}}{{\sqrt 2 }}} \right)$
D. None of these

Answer 1

In this question, we need to determine the acceleration of the charged particle at the point of its emergence at the other side such that it enters the region of the magnetic field $\vec B = B\hat z$ with a velocity $\vec v = v\hat i$. For this, we will follow the concept of the particle moving in a uniform magnetic field and also, use Newton’s equation of motion to evaluate the acceleration of the particle at the emergence.

Complete step by step answer:
When a charged particle enters into a uniform magnetic field then, it will experience a force which will be the perpendicular to the plane containing the magnetic field and the velocity of the particle. The motion of the particle inside a magnetic field will be in a circular path with the radius is given by
$\dfrac{{m{v^2}}}{r} = Bvq \\\ r = \dfrac{{mv}}{{qB}} \\\$
According to the question, the diameter of the circular path followed by the particle is $d = \dfrac{{mv}}{{2qB}}$ as the magnetic field is present only in between y=0 to y=d.
Hence, we can write $r = 2d$.
Let $\theta$ be the angle of emergence of the particle from the magnetic field after which it will follow a straight-line path.
The following figure depicts the pictorial representation of the motion of the particle from the point of entrance in the magnetic field to the point of emergence of the magnetic field.

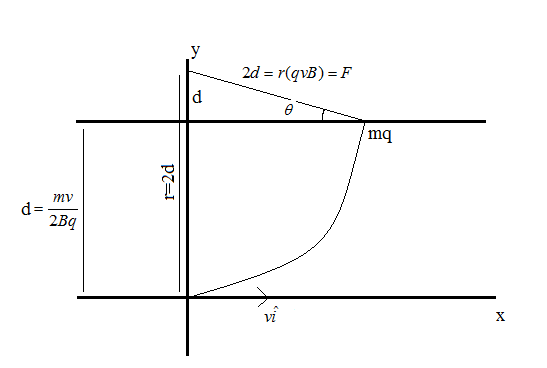
From the figure, we can see that
$\sin \theta = \dfrac{d}{{2d}} \\\ = \dfrac{1}{2} \\\$
Taking sin inverse to both sides of the above equation
${\sin ^{ - 1}}(\sin \theta ) = {\sin ^{ - 1}}\left( {\dfrac{1}{2}} \right) \\\ \theta = \dfrac{\pi }{6} \\\$
Hence, the angle at which the particle exists from the magnetic field is $\dfrac{\pi }{6}$.
The force on the particle moving in a magnetic field is given by
$F = q\left( {\vec v \times \vec B} \right) \\\ \implies ma = q\left( {\vec v \times \vec B} \right) \\\ \implies a = \dfrac{{q\left( {\vec v \times \vec B} \right)}}{m} \\\$
Substituting the value of the velocity as $\vec v = \cos \theta \hat i - \sin \theta \hat j$ in the above equation

$$a = \dfrac{{q\left( {\vec v \times \vec B} \right)}}{m} \\\ = \dfrac{q}{m}\left[ {\left( {\cos \theta \hat i - \sin \theta \hat j} \right) \times B\hat k} \right] \\\ = \dfrac{{qvB}}{m}\left[ { - \cos \theta \hat i + \sin \theta \hat j} \right] \\\$$

Substituting the value of $\theta$ as $\dfrac{\pi }{6}$ in the above equation, we get

$$a = \dfrac{{qvB}}{m}\left[ { - \cos \left( {\dfrac{\pi }{6}} \right)\hat i + \sin \left( {\dfrac{\pi }{6}} \right)\hat j} \right] \\\ = \dfrac{{qvB}}{m}\left[ { - \dfrac{{\sqrt 3 }}{2}\hat i + \dfrac{1}{2}\hat j} \right] \\\$$

Hence, the acceleration of the particle at the point of emergence from the magnetic field is given by $\dfrac{{qvB}}{m}\left[ { - \dfrac{{\sqrt 3 }}{2}\hat i + \dfrac{1}{2}\hat j} \right]$

So, the correct answer is “Option D”.

Note:
It is interesting to note here that the particle will follow the circular path only when it is under the influence of the magnetic field. As soon as the magnetic field is removed, the particle will follow a straight-line path.