Question
Question: The refractive indices of flint glass prisms for \(C,D\) and \(F\) lines are \(1.790,1.795\) and \(1...
The refractive indices of flint glass prisms for C,D and F lines are 1.790,1.795 and 1.805 respectively. The dispersive power of the flint glass prism is
A)0.141B)0.125C)0.018D)0.929
Solution
Dispersive power of a prism is defined as the ratio of angular dispersion to the angle of deviation for the mean wavelength. C,D and F lines of a prism correspond to red, yellow and violet lines of the prism. Angle of deviation of a particular color of light when passed through a prism is dependent on the refractive index of that particular color of light.
Formula used:
ω=δyδv−δr=μy−1μv−μr
Complete step by step answer:
Dispersive power of the material of a prism refers to the ratio of angular dispersion to the angle of deviation for the mean wavelength. Here, angle of deviation for the mean wavelength corresponds to the yellow line of the prism. C,D and F lines of a prism correspond to red, yellow and violet lines of the prism. Mathematically, dispersive power of a prism is given by
ω=δyδv−δr
where
ω is the dispersive power of a prism
δv is the angle of deviation of violet light
δr is the angle of deviation of red light
δy is the angle of deviation of yellow light (mean wavelength)
δv−δr refers to the angular dispersion of the prism
Let this be equation 1.
The figure given below can be referred for clarity.
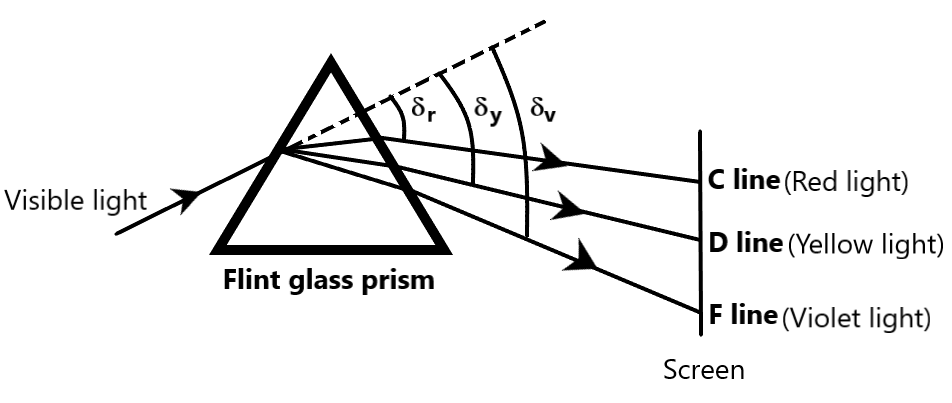
Since angular dispersion and angle of deviation for the mean wavelength are related to the respective refractive indices of red, yellow and violet lines of the prism, dispersive power of the prism is also related to the refractive indices of the mentioned. Therefore, equation 1 can be rewritten as
ω=δyδv−δr=μy−1μv−μr
where
μv is the refractive index corresponding to violet light or F line
μr is the refractive index corresponding to red light or C line
μy is the refractive index corresponding to yellow light or D line
Let this be equation 2.
Coming to our question, we are provided with a flint glass prism. It is also given that
μr=1.790, is the refractive index corresponding to C line of the flint glass prism
μv=1.805, is the refractive index corresponding to F line of the prism
μy=1.795, is the refractive index corresponding to D line of the prism
Substituting these values in equation 2, we have
ω=μy−1μv−μr=1.795−11.805−1.790=0.7950.015=0.018∘
Therefore, dispersive power of the given flint glass prism is equal to 0.018∘. The correct answer is option C.
Note:
The question can also be approached in a different way, using the formula given below:
ω=μD−1μF−μC
where
μF is the refractive index corresponding to F line
μC is the refractive index corresponding to C line
μD is the refractive index corresponding to D line
This can be considered as a direct approach to the question and students need not think about red, yellow and violet lines, here.
