Solveeit Logo
Login

Question

Question: The reflection of the point \(P\left( 1,0,0 \right)\) in the line \(\dfrac{x-1}{2}=\dfrac{y+1}{-3}=\...

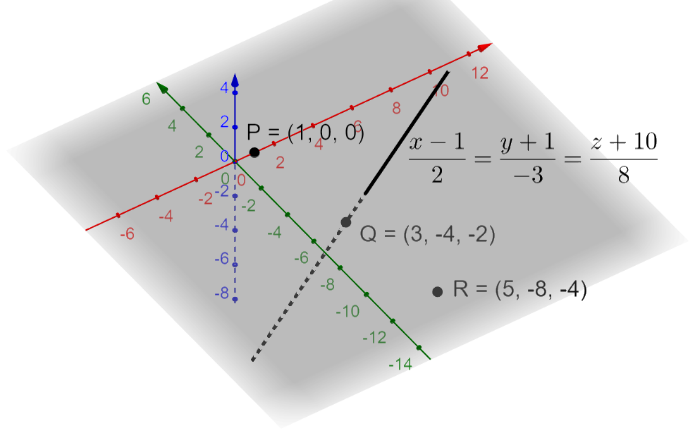
The reflection of the point P(1,0,0)P\left( 1,0,0 \right) in the line x−12=y+1−3=z+108\dfrac{x-1}{2}=\dfrac{y+1}{-3}=\dfrac{z+10}{8} is
(a) (3,−4,−2)\left( 3,-4,-2 \right)
(b) (5,−8,−4)\left( 5,-8,-4 \right)
(c) (1,−1,−10)\left( 1,-1,-10 \right)
(d) (2,−3,8)\left( 2,-3,8 \right)

Explanation

Solution

We start solving the problem by finding the D.R’s of the line x−12=y+1−3=z+108\dfrac{x-1}{2}=\dfrac{y+1}{-3}=\dfrac{z+10}{8} using the fact that the D.R’s (Direction Ratios) of the line of the form x−ad=y−be=z−cf\dfrac{x-a}{d}=\dfrac{y-b}{e}=\dfrac{z-c}{f} is (d,e,f)\left( d,e,f \right). We then find the general form of the point that lies on the given line x−12=y+1−3=z+108\dfrac{x-1}{2}=\dfrac{y+1}{-3}=\dfrac{z+10}{8} by equating it to a constant. We then find the D.R’s of the line passing through point P and with foot of perpendicular on the given line. We then use the fact that if two lines with D.R’s (x1,y1,z1)\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right) and (x2,y2,z2)\left( {{x}_{2}},{{y}_{2}},{{z}_{2}} \right) are perpendicular to each other, then x1x2+y1y2+z1z2=0{{x}_{1}}{{x}_{2}}+{{y}_{1}}{{y}_{2}}+{{z}_{1}}{{z}_{2}}=0 to find point Q. We then find the point of reflection by using the fact that Q is the mid-point of P and its reflection.

Complete step by step answer:
According to the problem, we are asked to find the reflection of the point P(1,0,0)P\left( 1,0,0 \right) in the line x−12=y+1−3=z+108\dfrac{x-1}{2}=\dfrac{y+1}{-3}=\dfrac{z+10}{8}.

We know that the D.R’s (Direction Ratios) of the line of the form x−ad=y−be=z−cf\dfrac{x-a}{d}=\dfrac{y-b}{e}=\dfrac{z-c}{f} is (d,e,f)\left( d,e,f \right).
So, the D.R’s of the line x−12=y+1−3=z+108\dfrac{x-1}{2}=\dfrac{y+1}{-3}=\dfrac{z+10}{8} is (2,−3,8)\left( 2,-3,8 \right) ---(1).
Now, let us find the common form of the points that were present on the line x−12=y+1−3=z+108\dfrac{x-1}{2}=\dfrac{y+1}{-3}=\dfrac{z+10}{8}.
So, let us assume x−12=y+1−3=z+108=r\dfrac{x-1}{2}=\dfrac{y+1}{-3}=\dfrac{z+10}{8}=r.
⇒x−12=r\Rightarrow \dfrac{x-1}{2}=r, y+1−3=r\dfrac{y+1}{-3}=r, z+108=r\dfrac{z+10}{8}=r.
⇒x−1=2r\Rightarrow x-1=2r, y+1=−3ry+1=-3r, z+10=8rz+10=8r.
⇒x=1+2r\Rightarrow x=1+2r, y=−1−3ry=-1-3r, z=−10+8rz=-10+8r.
So, the general form of the points which lies on the line x−12=y+1−3=z+108\dfrac{x-1}{2}=\dfrac{y+1}{-3}=\dfrac{z+10}{8} is (1+2r,−1−3r,−10+8r)\left( 1+2r,-1-3r,-10+8r \right).
So, let us assume the point Q(1+2r,−1−3r,−10+8r)Q\left( 1+2r,-1-3r,-10+8r \right) which lies on the line x−12=y+1−3=z+108\dfrac{x-1}{2}=\dfrac{y+1}{-3}=\dfrac{z+10}{8} and perpendicular to the line passing through the points P and Q, where Q is the foot of perpendicular the line joining PQ on the line x−12=y+1−3=z+108\dfrac{x-1}{2}=\dfrac{y+1}{-3}=\dfrac{z+10}{8}.
We know that the D.R’s of the line passing through (x1,y1,z1)\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right) and (x2,y2,z2)\left( {{x}_{2}},{{y}_{2}},{{z}_{2}} \right) is (x2−x1,y2−y1,z2−z1)\left( {{x}_{2}}-{{x}_{1}},{{y}_{2}}-{{y}_{1}},{{z}_{2}}-{{z}_{1}} \right).
So, we get the D.R’s of line PQ as (1+2r−1,−1−3r−0,−10+8r−0)=(2r,−1−3r,−10+8r)\left( 1+2r-1,-1-3r-0,-10+8r-0 \right)=\left( 2r,-1-3r,-10+8r \right).
So, the D.R’s of the line PQ is (2r,−1−3r,−10+8r)\left( 2r,-1-3r,-10+8r \right) ---(2).
So, we have line PQ perpendicular to x−12=y+1−3=z+108\dfrac{x-1}{2}=\dfrac{y+1}{-3}=\dfrac{z+10}{8}.
We know that if two lines with D.R’s (x1,y1,z1)\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right) and (x2,y2,z2)\left( {{x}_{2}},{{y}_{2}},{{z}_{2}} \right) are perpendicular to each other, then x1x2+y1y2+z1z2=0{{x}_{1}}{{x}_{2}}+{{y}_{1}}{{y}_{2}}+{{z}_{1}}{{z}_{2}}=0.
So, we have (2r×2)+((−1−3r)×−3)+((−10+8r)×8)=0\left( 2r\times 2 \right)+\left( \left( -1-3r \right)\times -3 \right)+\left( \left( -10+8r \right)\times 8 \right)=0.
⇒4r+3+9r−80+64r=0\Rightarrow 4r+3+9r-80+64r=0.
⇒77r−77=0\Rightarrow 77r-77=0.
⇒77r=77\Rightarrow 77r=77.
⇒r=1\Rightarrow r=1. Let us use this to find point Q.
So, we get point Q as Q(1+2(1),−1−3(1),−10+8(1))=Q(1+2,−1−3,−10+8)=Q(3,−4,−2)Q\left( 1+2\left( 1 \right),-1-3\left( 1 \right),-10+8\left( 1 \right) \right)=Q\left( 1+2,-1-3,-10+8 \right)=Q\left( 3,-4,-2 \right).
Now, let us assume the reflection of point P be R(a1,b1,c1)R\left( {{a}_{1}},{{b}_{1}},{{c}_{1}} \right). We know that the point Q is midpoint of the line PR.
So, we have (3,−4,−2)=(1+a12,0+b12,0+c12)\left( 3,-4,-2 \right)=\left( \dfrac{1+{{a}_{1}}}{2},\dfrac{0+{{b}_{1}}}{2},\dfrac{0+{{c}_{1}}}{2} \right).
⇒(3,−4,−2)=(1+a12,b12,c12)\Rightarrow \left( 3,-4,-2 \right)=\left( \dfrac{1+{{a}_{1}}}{2},\dfrac{{{b}_{1}}}{2},\dfrac{{{c}_{1}}}{2} \right).
⇒1+a12=3\Rightarrow \dfrac{1+{{a}_{1}}}{2}=3, b12=−4\dfrac{{{b}_{1}}}{2}=-4, c12=−2\dfrac{{{c}_{1}}}{2}=-2.
⇒1+a1=6\Rightarrow 1+{{a}_{1}}=6, b1=−8{{b}_{1}}=-8, c1=−4{{c}_{1}}=-4.
⇒a1=5\Rightarrow {{a}_{1}}=5, b1=−8{{b}_{1}}=-8, c1=−4{{c}_{1}}=-4.
So, we have found the reflection of point P as (5,−8,−4)\left( 5,-8,-4 \right).

So, the correct answer is “Option b”.

Note: We can see that the given problem contains a huge amount of calculation so, we need to perform each step carefully to avoid mistakes and confusion. Whenever we get this type of problem, we first start with finding D.R’s and general form of the point on the line to proceed into the problem. We should know that the line passing through the point P should be perpendicular in order to find the reflection. Similarly, we can expect problems to find the equation of the line passing through P and R.