Question

The reflection of $\left( { - 6, - 3} \right)$ on the $y$ axis has coordinates
A) $\left( { - 6,3} \right)$
B) $\left( {6, - 3} \right)$
C) $\left( {6,3} \right)$
D) $\left( { - 3,6} \right)$

Answer 1

Here, we will assume the $y$ axis as a mirror. We will plot the given point in its respective quadrant and draw a perpendicular towards the mirror. The distance between the point and the mirror or the length of the perpendicular will be equal to the distance between the image of the point and the mirror. We will use this fact and find the required coordinates of the reflection of the given point.

Complete step by step solution:
To find the reflection of $\left( { - 6, - 3} \right)$ on the $y$ axis:
First, we will draw the $x$ axis and $y$ axis respectively.
Then, we will mark the point $\left( { - 6, - 3} \right)$ keeping in mind that the $x$ coordinate is $- 6$ and the $y$ coordinate is $- 3$.
Now, according to the question, we have to find its reflection on the $y$ axis.
Hence, the $y$ axis would act as a mirror.
Therefore, we will draw a perpendicular from the point $\left( { - 6, - 3} \right)$ to the $y$ axis.

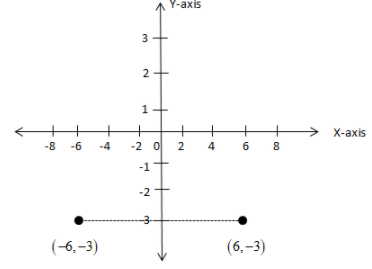
Now, we can see from the diagram that the length of the perpendicular drawn is 6 units. Here, we will not take the negative value of 6 because we are talking about length which can never be negative.
The distance of an object in front of the mirror and the distance of its image behind the mirror is always equal.
So, we will extend this perpendicular on the other side of the mirror i.e. the $y$ axis by 6 units.
Since, on the right hand side of the $y$ axis, the $x$ coordinate is always positive, hence, 6 will be positive in nature.
Also, in this question, the mirror was assumed to be the $y$ axis, hence, the coordinates of $y$ will remain the same.
Therefore, the reflection of $\left( { - 6, - 3} \right)$ on the $y$ axis has coordinates $\left( {6, - 3} \right)$.

Hence, option B is the correct answer.

Note:
Another way to solve this question is:
According to the question, we are given the point $\left( { - 6, - 3} \right)$ which lies in the third quadrant.
Since, the $y$ axis acts like a mirror.
Hence, its reflection will fall in the fourth quadrant where the $x$ coordinate is always positive and the $y$ coordinate is negative.
Therefore, clearly, the reflection of $\left( { - 6, - 3} \right)$ on the $y$ axis has coordinates$\left( {6, - 3} \right)$.