Question

The rectangular components of force $5dyne$ are:
A. $3$ and $4{\text{ }}dyne$.
B. $2.5$ and $25{\text{ }}dyne$.
C. $1$ and $2{\text{ }}dyne$.
D. $2$ and $3{\text{ }}dyne$.

Answer 1

The part of the vector which is resolved in vertical and horizontal components is known as rectangular components. Rectangular components are always perpendicular to each other.

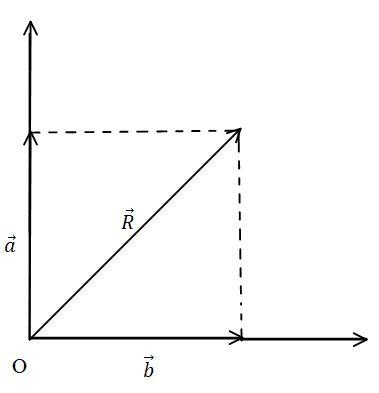
In this diagram $\overrightarrow a$ and $\overrightarrow b$ are rectangular components for $\overrightarrow R$.

Complete step by step answer:
Here, the rectangular components can be calculated by this diagram,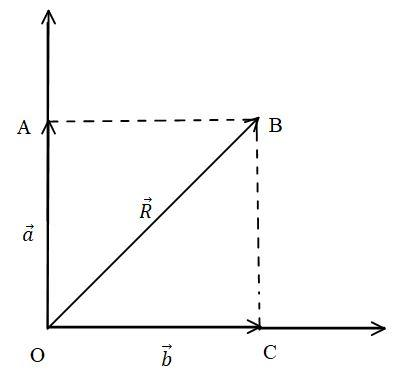
The values of ${\text{OC}} = b$ and ${\text{OA}} = a$ by applying Pythagoras we get, ${R^2} = \sqrt {{\text{O}}{{\text{A}}^2}{\text{ + O}}{{\text{C}}^2}}$ which gives,
$R = \sqrt {{a^2} + {b^2}}$.The rectangular components are the vertical and horizontal components of any vector and they are always perpendicular to each other. So we can check each option and see which is the correct option for this problem.
Let us consider the first option,
$3$ and $4{\text{ }}dyne$,
Here, let $a = 3$ and$b = 4$, using the relation $R = \sqrt {{a^2} + {b^2}}$, we can calculate the value of $R$ and if it matches the value given i.e. $5dyne$ then this may be the right option,
$R = \sqrt {{a^2} + {b^2}}$
Put $a = 3$ and$b = 4$ in above equation,
$R = \sqrt {{a^2} + {b^2}} \\\ \Rightarrow R = \sqrt {{3^2} + {4^2}} \\\ \Rightarrow R = \sqrt {9 + 16} \\\ \Rightarrow R = \sqrt {25} \\\ \Rightarrow R = 5 \\\$
So, the value of $R = 5dyne$.........eq. (1)
Let us check second option,
$2.5$ and $25{\text{ }}dyne$.
Here, let $a = 2.5$ and $b = 25$, using the relation $R = \sqrt {{a^2} + {b^2}}$, we can calculate the value of $R$ and if it matches the value given i.e. $5dyne$ then this may be the right option,
$R = \sqrt {{a^2} + {b^2}}$
Put $a = 2.5$ and$b = 25$ in above equation,
$R = \sqrt {{a^2} + {b^2}} \\\ \Rightarrow R = \sqrt {{{\left( {2.5} \right)}^2} + {{25}^2}} \\\ \Rightarrow R = \sqrt {6.25 + 625} \\\ \Rightarrow R = \sqrt {631.25} \\\ \Rightarrow R = 25.13 \\\$
So, the value of $R = 25.13dyne$..........eq (2)
Let us check third option,
$1$ and$2{\text{ }}dyne$,
Here, let $a = 1$ and $b = 2$, using the relation $R = \sqrt {{a^2} + {b^2}}$, we can calculate the value of$R$ and if it matches the value given i.e. $5dyne$ then this may be the right option,
$R = \sqrt {{a^2} + {b^2}}$
Put $a = 1$ and $b = 2$ in above equation,
$R = \sqrt {{a^2} + {b^2}} \\\ \Rightarrow R = \sqrt {{1^2} + {2^2}} \\\ \Rightarrow R = \sqrt {1 + 4} \\\ \Rightarrow R = \sqrt 5 \\\ \Rightarrow R = 2.236 \\\$
So, the value of $R = 2.236dyne$.........eq. (3)
Let us check forth and last option,
$2$and$3{\text{ }}dyne$.
Here, let $a = 2$ and $b = 3$, using the relation$R = \sqrt {{a^2} + {b^2}}$, we can calculate the value of $R$ and if it matches the value given i.e. $5dyne$ then this may be the right option,
$R = \sqrt {{a^2} + {b^2}}$
Put $a = 2$ and$b = 3$ in above equation,
$R = \sqrt {{a^2} + {b^2}} \\\ \Rightarrow R = \sqrt {{2^2} + {3^2}} \\\ \Rightarrow R = \sqrt {4 + 9} \\\ \Rightarrow R = \sqrt {13} \\\ \Rightarrow R = 3.61 \\\$
So, the value of $R = 3.61dyne$.........eq. (4)
$\therefore$ From equations (1), (2), (3) and (4) it is clear that option A is the correct answer.

Note: Students should not get confuse while calculating rectangular components, the rectangular components are always perpendicular and in this relation $R = \sqrt {{a^2} + {b^2}}$ $a$ and $b$ are the rectangular components, where $R$ is the magnitude of the vector. Also Dyne is just a unit for Force like Newton.