Question

The ratio of packing density in fcc, bcc and cubic structure is respectively ______.
(A) 1 : 0.92 : 0.70
(B) 0.70 : 0.92 : 1
(C) 1 : 0.70 : 0.92
(D) 0.92 : 0.70 : 1

Answer 1

Draw the diagram of a simple cubic, FCC and BCC unit cells. Each side of a simple cubic cell has length which equals two radii of two adjacent atoms. Volume of a sphere is equal to $\dfrac{4}{3}\pi {{r}^{3}}$.

Complete step by step answer:
For a simple cubic cell,

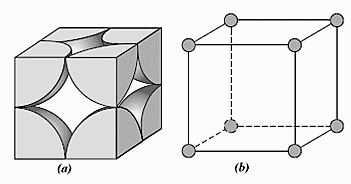
Length of each side of cubic cell, a=2r
Volume of one atom having radius (r) = $\dfrac{4}{3}\pi {{r}^{3}}$
There are 8 atoms occupying the corners of the cube. Each corner contains only $\dfrac{1}{8}th$ of an atom because one atom is surrounded by eight atoms. So, the total number of atoms present in a simple cubic cell $=\dfrac{1}{8}\times 8=1$.
Total volume of a unit cell $={{\left( 2r \right)}^{3}}=8{{r}^{3}}$
If an atom occupies the entire volume then, the volume occupied will be 100%. Now, the cubic cell contains only one atom and one atom can occupy only $\dfrac{4}{3}\pi {{r}^{3}}$ of volume. So, packing efficiency is $\dfrac{\dfrac{4}{3}\pi {{r}^{3}}}{8{{r}^{3}}}\times 100=52.4$

Similarly, let us calculate for BCC unit cell,

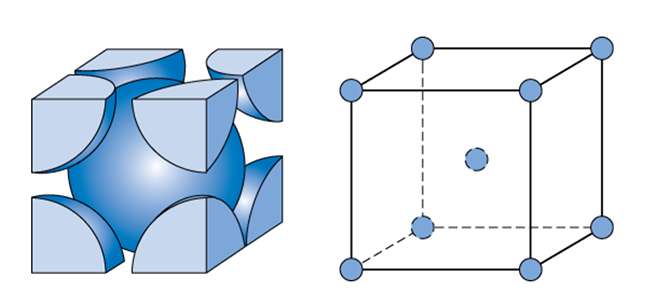
One atom is present in the centre of the unit cell and there are eight atoms present on the corners. Each corner contributes $\dfrac{1}{8}th$ of an atom because one atom is surrounded by eight atoms. So, the total number of atoms present in a simple cubic cell $=\left( \dfrac{1}{8}\times 8 \right)+1=2$.
Volume occupied by two atoms in the BCC unit cell $=2\times \dfrac{4}{3}\pi {{r}^{3}}=\dfrac{8}{3}\pi {{r}^{3}}$
In a BCC unit cell, consider AD as the diagonal of the cube and AB as the diagonal of a side of a cube. Consider a right-angled triangle ABC, where (length of the side of the cube). Applying Pythagoras theorem to $\vartriangle ABC$, ${{\left( AB \right)}^{2}}={{\left( AC \right)}^{2}}+{{\left( BC \right)}^{2}}=2{{a}^{2}}$.
Similarly, consider a right-angled triangle $\vartriangle ABD$, where , ${{\left( AB \right)}^{2}}=2{{a}^{2}}$
$\begin{aligned} & {{\left( AD \right)}^{2}}={{\left( AB \right)}^{2}}+{{\left( BD \right)}^{2}} \\\ & =2{{a}^{2}}+{{a}^{2}} \\\ & =3{{a}^{2}} \\\ & AD=\sqrt{3}a \end{aligned}$
But we know, the length of diagonal AD is 4r due to the presence of two radii of corner atoms and one diameter of central atom. So, equating the two values,
$AD=\sqrt{3}a=4r$
$\therefore a=\dfrac{4}{\sqrt{3}}r$
The total volume of cube $={{a}^{3}}=\dfrac{64}{3\sqrt{3}}{{r}^{3}}$
Therefore, packing efficiency of BCC unit cell is $\dfrac{8}{3}\pi {{r}^{3}}\times \dfrac{3\sqrt{3}}{64{{r}^{3}}}\times 100=68.09$

Similarly, let’s calculate for FCC cells.

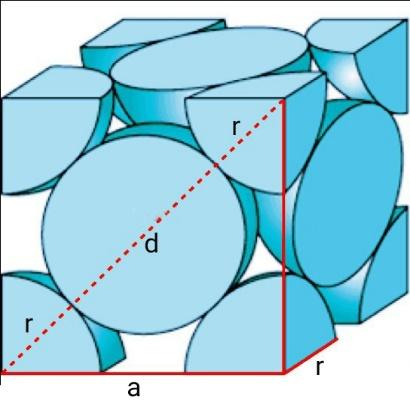
The FCC cell contains $\dfrac{1}{8}th$ atom at the 8 corners and $\dfrac{1}{2}th$ atom at the six faces.
Therefore, total atoms in a FCC cell $=\dfrac{1}{8}\times 8+\dfrac{1}{2}\times 6=4$.
Consider a right-angled triangle $\vartriangle ABC$ on the face of a FCC cell, where AC=BC=a and AB=4r. Similarly, ${{\left( AB \right)}^{2}}={{\left( AC \right)}^{2}}+{{\left( BC \right)}^{2}}={{a}^{2}}+{{a}^{2}}=2{{a}^{2}}=16{{r}^{2}}$
Therefore, $a=\sqrt{8}r$
Volume of the FCC unit cell $={{a}^{3}}=8\sqrt{8}{{r}^{3}}$
Actual volume occupied by a cube of FCC $=4\times \dfrac{4}{3}\pi {{r}^{3}}=\dfrac{16}{3}\pi {{r}^{3}}$
Hence, packing efficiency of FCC unit cell is $\dfrac{16}{3}\pi {{r}^{3}}\times \dfrac{1}{8\sqrt{8}{{r}^{3}}}\times 100=74.0$
Now taking the ratio of all the three we get, FCC : BCC : SC=1 : 0.92 : 0.70
So, the correct answer is “Option A”.

Note: Systematically calculate the volume occupied by atoms in each of the unit cells. Empty space or void in each cell can be calculated as well by just subtracting packing efficiency by a factor of 100.