Question

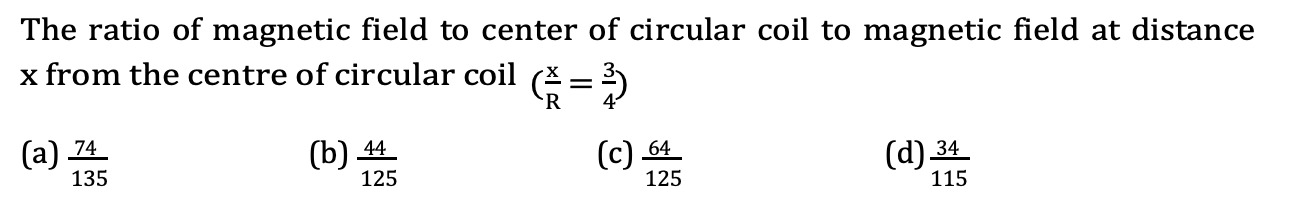
The ratio of magnetic field to center of circular coil to magnetic field at distance x from the centre of circular coil ($\frac{x}{R}=\frac{3}{4}$)

• A. $\frac{74}{135}$
• B. $\frac{44}{125}$
• C. $\frac{64}{125}$
• D. $\frac{34}{115}$

Answer 1

Answer: (C)

$\frac{64}{125}$

Answer 2

The magnetic field along the axis of a current loop is given by

$$B(x) = \frac{\mu_0 I R^2}{2\left(R^2+x^2\right)^{3/2}}$$

and at the center,

$$B(0) = \frac{\mu_0 I}{2R}.$$

Thus, the ratio (considering the field at $x$ relative to that at the center) is

$$\frac{B(x)}{B(0)} = \frac{\frac{\mu_0 I R^2}{2\left(R^2+x^2\right)^{3/2}}}{\frac{\mu_0 I}{2R}} = \frac{R^3}{\left(R^2+x^2\right)^{3/2}}.$$

Given $\frac{x}{R}=\frac{3}{4}$, so $x=\frac{3}{4}R$. Therefore:

$$R^2 + x^2 = R^2 + \left(\frac{3}{4}R\right)^2 = R^2 + \frac{9}{16}R^2 = \frac{25}{16}R^2.$$

Taking the power,

$$\left(R^2+x^2\right)^{3/2} = \left(\frac{25}{16}R^2\right)^{3/2} = \left(\frac{25}{16}\right)^{3/2} R^3 = \frac{125}{64}\, R^3.$$

Thus, the ratio becomes:

$$\frac{B(x)}{B(0)} = \frac{R^3}{\frac{125}{64}\, R^3} = \frac{64}{125}.$$