Question

The ratio of magnetic dipole moment to angular momentum in hydrogen like atom is :-

& a)\dfrac{e}{m} \\\ & b)\dfrac{e}{2m} \\\ & c)\dfrac{e}{3m} \\\ & d)\dfrac{2e}{m} \\\ \end{aligned}$$

Answer 1

When electron revolves in the circular orbit then that orbit will behave like a current carrying loop due to motion of electron and this current carrying loop has poles like magnet so it behaves like magnetic dipole. Then we use the general relation for magnetic moment and angular momentum for finding the ratio.

Complete answer:
An electron is revolving in an orbit about the nucleus of a hydrogen-like atom which behaves like a current loop and produces a magnetic field. So this current carrying loop behaves like magnetic dipole because its properties are matching with the properties of a magnet.

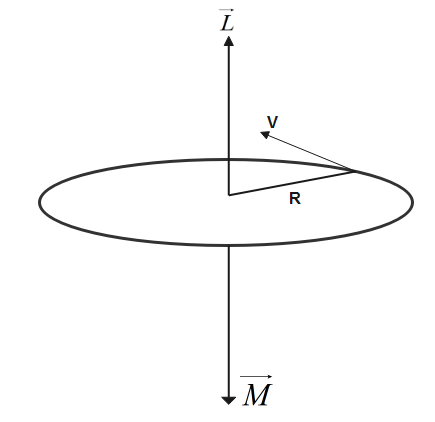
Let us assume the mass of electron revolving is m.
Let us assume the charge of a revolving electron is e.
An electron of mass m and charge is moving with speed v in a circular orbit of radius R. Due to motion of electrons in the loop it behaves like a current carrying loop.
Now we calculate the current I produced in the loop in time period of T is represented by formula.
According to formula,
$i=\dfrac{e}{T}$Equation 1
Where T is the time period of revolution.
So $Time(T)=\dfrac{Dis\tan ce}{Speed}$
$\Rightarrow T=\dfrac{2\pi R}{v}$
Put the value of time period T in equation 1 is given by the equation -
$i=\dfrac{ev}{2\pi R}$(Equation2)
Let us assume Magnetic moment due to current carrying loop is represented by M
so formula for magnetic moment will be-
$M=iA$
Where A be the area of orbit of radius r.
So put the value of current i from equation 2 and area of loop A we get,

& \Rightarrow M=\dfrac{ev}{2\pi R}\times \pi {{R}^{2}} \\\ & \therefore M=\dfrac{evR}{2} \\\ \end{aligned}$$ The magnitude of angular momentum L of revolving electron in orbit of radius R is given by $$L=mvR$$ Now we calculate the ratio of Magnetic moment and angular momentum we get, $$\dfrac{M}{L}=\dfrac{evR}{2mvR}$$ On Simplifying ,we get $$\therefore \dfrac{M}{L}=\dfrac{e}{2m}=cons\operatorname{tant}$$ The ratio of Magnitude of magnetic dipole moment to the magnitude of angular momentum of a revolving electron is a constant, independent of the other parameters of orbit. This ratio is called the gyromagnetic ratio for the electron. **So Correct Option is B.** **Note:** The direction of magnetic dipole moment and angular momentum is identified by Right hand thumb rule. Current is responsible for finding the direction of magnetic dipole moment and mass is responsible for finding the current of angular momentum so direction of magnetic dipole momentum is downwards while that of direction of angular momentum is upwards.