Question
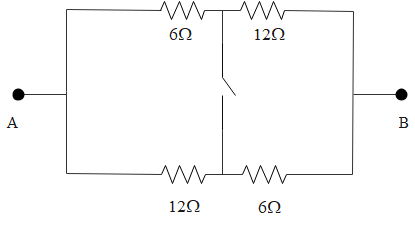
Question: The ratio of equivalent resistance across A and B when switch is open to that when switch is closed ...
The ratio of equivalent resistance across A and B when switch is open to that when switch is closed is:
(A) 83
(B) 85
(C) 87
(D) 89
Solution
Hint
We know that the equivalent resistance is where the aggregate resistance connected either in parallel or series is calculated. More resistance means less current is flowing through the circuit. Equivalent resistance is a different way of indicating total resistance, which we calculate differently for series and parallel circuits. In a series circuit, the different components are connected in a single, continuous loop. However, if we had a huge and complicated circuit with many resistors, then the effective resistance is the total resistance of the circuit. Effective resistance is usually measured between 2 points. Based on this concept we have to solve this question.
Complete step by step answer
We can see from the question that,
When switch is open:
6Ω and 12Ω are connected in series and 12Ω and 6Ω are also connected in series and both these are in parallel connection. So,
RAB=(6+12)∥(12+6)
⇒RAB=18∥18=9Ω
When switch is closed:
6Ω and 12Ω are connected in parallel and 12Ω and 6Ω are also connected in parallel and both these are in series connection.
So, RAB′=[6∥12]+[12∥6]
Or, 6∥12=6+126×12=4Ω
Or, RAB′=4+4=8Ω
The Ratio can be calculated as,
RAB′RAB=89
Therefore, the correct answer is Option (D).
Note
We know that in a series circuit, the output current of the first resistor flows into the input of the second resistor; therefore, the current is the same in each resistor. In a parallel circuit, all of the resistor leads on one side of the resistors are connected together and all the leads on the other side are connected together. As more and more resistors are added in parallel to a circuit, the equivalent resistance of the circuit decreases and the total current of the circuit increases. Adding more resistors in parallel is equivalent to providing more branches through which charge can flow. In a series circuit, the effective resistance is equal to the sum of the resistances of individual components. So total resistance will be on the higher side. In parallel circuit, reciprocal of effective resistance is equal to sum of reciprocals of individual resistances. So effective resistance is less.
