Question

The ratio of area of the circumcircle to that of the in circle in equilateral triangle is
(a) 2 : 1
(b) 3 : 2
(c) 4 : 1
(d) 9 : 1

Answer 1

Hint: In this question, we first need to find the semi perimeter of the triangle given by the formula $s=\dfrac{a+b+c}{2}$. Then, we get the area of the equilateral triangle which is given by the formula $\Delta =\dfrac{\sqrt{3}}{4}{{a}^{2}}$. Now, we need to find the radius of the incircle and circumcircle which are given by the formula $r=\dfrac{\Delta }{s}$ and $R=\dfrac{abc}{4\Delta }$. Now, on further calculating the areas of the respective circles and finding their ratio we get the result.

Complete step-by-step answer:
Let us assume the side of the equilateral triangle as a and it's in radius as r and circumradius as R
Now let us calculate the semi perimeter of the equilateral triangle using the formula
$s=\dfrac{a+b+c}{2}$
Now, on substituting the respective sides we get,
$s=\dfrac{a+a+a}{2}$
Now, on further simplification we get,
$\therefore s=\dfrac{3a}{2}$
As we already know that the area of an equilateral triangle with side a is given by
$\Delta =\dfrac{\sqrt{3}}{4}{{a}^{2}}$

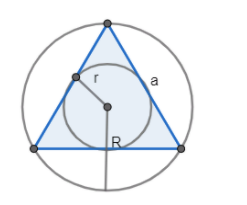
Now, the relation between the in circle and the area of the triangle and semi perimeter is given by the formula
$\Rightarrow r=\dfrac{\Delta }{s}$
Now, on substituting the respective values of the area and semi perimeter in the above formula we get,
$\Rightarrow r=\dfrac{\dfrac{\sqrt{3}}{4}{{a}^{2}}}{\dfrac{3a}{2}}$
Now, this can be further written in the simplified form as
$\Rightarrow r=\dfrac{\sqrt{3}{{a}^{2}}}{4}\times \dfrac{2}{3a}$
Now, on cancelling out the common terms in the above expression we get,
$\therefore r=\dfrac{a}{2\sqrt{3}}$
Now, as we already know that the relation between the circumradius and the sides of the triangle and the area is given by the formula
$\Rightarrow R=\dfrac{abc}{4\Delta }$
Now, on further substituting the respective values of the sides and area we get,
$\Rightarrow R=\dfrac{a\times a\times a}{4\times \dfrac{\sqrt{3}{{a}^{2}}}{4}}$
Now, this can be further written in the simplified form as
$\Rightarrow R=\dfrac{4{{a}^{3}}}{4\sqrt{3}{{a}^{2}}}$
Now, on cancelling out the common terms and simplifying further we get,
$\therefore R=\dfrac{a}{\sqrt{3}}$
Now, the ratio of the area of the circumcircle and the in circle is given by
$\Rightarrow \pi {{R}^{2}}:\pi {{r}^{2}}$
Now, on taking out the common term we get,
$\Rightarrow {{R}^{2}}:{{r}^{2}}$
Now, on further substituting the respective values we get,
$\Rightarrow {{\left( \dfrac{a}{\sqrt{3}} \right)}^{2}}:{{\left( \dfrac{a}{2\sqrt{3}} \right)}^{2}}$
Now, on further simplification we get,
$\Rightarrow \dfrac{{{a}^{2}}}{3}:\dfrac{{{a}^{2}}}{4\times 3}$
Now, on cancelling out the common terms we get,
$\Rightarrow 1:\dfrac{1}{4}$
Now, this can be further written in the simplified form as
$\Rightarrow 4:1$
Hence, the correct option is (c).

Note: Instead of using the relation between the respective radii and the area, semi perimeter and the sides we can also get their values by using geometry and simplify further. Both the methods give the same result but this would be lengthy.
It is important to note that the circum radius depends on area and sides directly whereas the in radius depends on semi perimeter and area. Because considering their values in the other way completely changes the result.
It is also to be noted that the circumradius should be greater than the in radius as the circumcircle lies outside the triangle and the circle lies inside the triangle.