Question

The ratio in which the plane $r\cdot \left( \overline{i}-2\overline{j}+3\overline{k} \right)=17$ divides the line joining the points $-2\hat{i}+4\hat{j}+7\hat{k}$ and $3\hat{i}-5\hat{j}+8\hat{k}$ is
(a) $1:5$
(b) $1:10$
(c) $3:5$
(d) $3:10$

Answer 1

First, we will find midpoint using the section formula given as $\dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n}$ where we will assume $m:n$ to be $\lambda :1$ . Here, for finding point i, we will use respective values of i from point $-2\hat{i}+4\hat{j}+7\hat{k}$ and $3\hat{i}-5\hat{j}+8\hat{k}$ which is $\left( -2,3 \right)$ . Similarly for point j, point will be $\left( 4,-5 \right)$ and for point k it is $\left( 7,8 \right)$ . The, we will place those values in the plane equation i.e. $r\cdot \left( \overline{i}-2\overline{j}+3\overline{k} \right)=17$ and then on solving we will get a value of $\lambda$ which will be the answer.

Complete step by step answer:
Here, we will draw a figure to understand clearly.

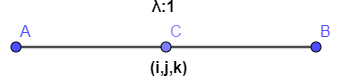
We have assumed the ratio which divides the plane to be $\lambda :1$ which is the same to be $m:n$ . Also, point A is $-2\hat{i}+4\hat{j}+7\hat{k}$ and point B is $3\hat{i}-5\hat{j}+8\hat{k}$ .
Here, for finding point i, we will use respective values of i from point $-2\hat{i}+4\hat{j}+7\hat{k}$ and $3\hat{i}-5\hat{j}+8\hat{k}$ which is $\left( -2,3 \right)$ . Similarly for point j, point will be $\left( 4,-5 \right)$ and for point k it is $\left( 7,8 \right)$ .
Now, we will use section formula to find midpoints of the line which is given as $\dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n}$ . So, here we get i as
$i=\dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n}$
On substituting the values i.e. $\left( -2,3 \right)$ where ${{x}_{2}}=3,{{x}_{1}}=-2$ , we get as
$i=\dfrac{\lambda 3+1\left( -2 \right)}{\lambda +1}=\dfrac{3\lambda -2}{\lambda +1}$ …………………………….(1)
Similarly, we will find point j as $\left( 4,-5 \right)$ i.e. ${{x}_{2}}=-5,{{x}_{1}}=3$ we will get
$j=\dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n}$
On putting values, we get
$j=\dfrac{-5\lambda +1\left( 4 \right)}{\lambda +1}=\dfrac{-5\lambda +4}{\lambda +1}$ ………………………………(2)
Similarly, point k i.e. $\left( 7,8 \right)$ i.e. ${{x}_{2}}=8,{{x}_{1}}=7$ we will find as
$k=\dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n}$
On putting values, we will get
$k=\dfrac{8\lambda +1\left( 7 \right)}{\lambda +1}=\dfrac{8\lambda +7}{\lambda +1}$ …………………………….(3)
Now, all the three points i.e. i, j, k lies in the plane given as $r\cdot \left( \overline{i}-2\overline{j}+3\overline{k} \right)=17$ . So, we will substitute values of equation (1), (2), (3) in the given plane. So, we will get as
$\Rightarrow \dfrac{3\lambda -2}{\lambda +1}-2\left( \dfrac{-5\lambda +4}{\lambda +1} \right)+3\left( \dfrac{8\lambda +7}{\lambda +1} \right)=17$
On further solving, we will get as
$\Rightarrow \dfrac{3\lambda -2}{\lambda +1}+\dfrac{10\lambda -8}{\lambda +1}+\dfrac{24\lambda +21}{\lambda +1}=17$
$\Rightarrow 3\lambda -2+10\lambda -8+24\lambda +21=17\left( \lambda +1 \right)$
On simplification, we get equation as
$\Rightarrow 37\lambda +11=17\lambda +17$
Now, taking constant term on RHS and variable term on LHS, we will get
$\Rightarrow 37\lambda -17\lambda =17-11=6$
$\Rightarrow 20\lambda =6$
On dividing both sides by 20, we will get
$\Rightarrow \lambda =\dfrac{6}{20}=\dfrac{3}{10}$
Thus, the ratio in which the plane is divided is $3:10$ .
Hence, option (d) is the correct answer.

Note: Students should know the section formula which has to be used here in this problem. Students sometimes take the ratio as $1:\lambda$ and by doing this, we will get the same answer. We will get on solving, equation as $\dfrac{3-2\lambda }{\lambda +1}+\dfrac{10-8\lambda }{\lambda +1}+\dfrac{24+21\lambda }{\lambda +1}=17$ . On solving this we will get value as $\lambda =10:3$ . But remember that we have taken the ratio as $1:\lambda$ so, it will be $\dfrac{1}{\lambda }=\dfrac{10}{3}$ . Thus, we will get the same answer $3:10$ as $\lambda$ is in the denominator, so the ratio will be inverse. Do not write answers as $\lambda =10:3$ which will be wrong.