Question

The ratio in which the line joining the points (6, 4) and (1, −7) is divided by x-axis is
A) 1:3
B) 4:7
C) 2:7
D) 6:7

Answer 1

Hint : To find the ratio in which line joining two points is divided, we can use the section formula. We can substitute all the known coordinates in the formula and then by comparison of corresponding coordinates we can find the required ratio.
sectional formula is given as:
If the points A and B have coordinates $\left( {{x_1},{y_1}} \right)$ and $\left( {{x_2},{y_2}} \right)$ respectively. C (x, y) the point dividing this line in the ratio m:n, then:
$C\left( {x,y} \right) = \left( {\dfrac{{m{x_2} + n{x_1}}}{{m + n}},{\text{ }}\dfrac{{m{y_2} + n{y_1}}}{{m + n}}} \right)$

Complete step-by-step answer :
We have been given the coordinates of the two points. Let these points be A and B
A (6, 4)
B (1, −7)
Let the point lying on the x axis where the axis intersects with the line be (x, y). but as this point lies on the x – axis, its y coordinate will be 0. Let this point be X
X (x, 0)
Let the ratio in which the line gets divided by the axis be k:1

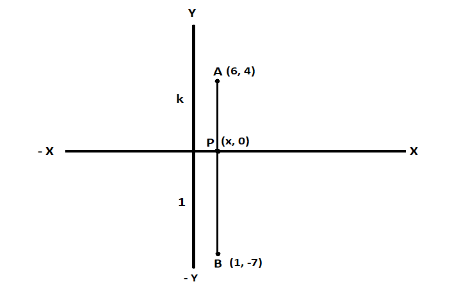
Applying the sectional formula:
If the points A and B have coordinates $\left( {{x_1},{y_1}} \right)$ and $\left( {{x_2},{y_2}} \right)$ respectively. C (x, y) the point dividing this line in the ratio m:n, then according to the sectional formula:
$C\left( {x,y} \right) = \left( {\dfrac{{m{x_2} + n{x_1}}}{{m + n}},{\text{ }}\dfrac{{m{y_2} + n{y_1}}}{{m + n}}} \right)$
Here,
${x_1} = 6 \\\ {x_2} = 1 \\\$
${y_1} = 4 \\\ {y_1} = - 7 \\\$
$x = x \\\ y = 0 \\\$
$m = k \\\ n = 1 \\\$
Substituting the values, we get:
$X\left( {x,0} \right) = \left( {\dfrac{{k + 6}}{{k + 1}},{\text{ }}\dfrac{{ - 7k + 4}}{{k + 1}}} \right)$
As one of the coordinates on LHS of the equation is 0, so we will use that for comparison.
So, comparing the y coordinates of both the sides of the equation, we get:
$\Rightarrow \dfrac{{ - 7k + 4}}{{k + 1}} = 0 \\\ \Rightarrow - 7k + 4 = 0 \\\ \Rightarrow - 7k = - 4 \\\ \Rightarrow k = \dfrac{4}{7} \\\$
The required ratio will be given as:
$k:1 = \dfrac{k}{1} \\\ \Rightarrow \dfrac{{\dfrac{4}{7}}}{1}{\text{ }}\left( {k = \dfrac{4}{7}} \right) \\\ \Rightarrow 4:7 \\\$
Therefore, the ratio in which the line joining the points (6, 4) and (1, −7) is divided by x-axis is $4:7$ and the correct option is B)
So, the correct answer is “Option B”.

Note : We can also take the ratio is m:n but that would just increase the calculation. When we take the ratio k:1 it means $\dfrac{{\dfrac{m}{n}}}{1}$ as the ratio of m and n can be equal to any constant k. so taking k:1 as the ratio makes no difference but decrease the calculative portion.
The ratio in terms of fraction can be written as:
$a:b = \dfrac{a}{b}$
If this point which divides the line segment is midpoint, then the ratio in which the line gets divided is 1:1