Question

The ratio in which $i + 2j + 3k$ divides the join of $- 2i + 3j + 5k$ and $7i - k$ is?
A.$- 3:2$
B.$1:2$
C.$2:3$
D.$- 4:3$

Answer 1

First we will first assume that $m$ is the ratio in which $i + 2j + 3k$ divides the join of $- 2i + 3j + 5k$ and $7i - k$. Then we will find the coordinates for the given equations and then we will simplify the equation $\dfrac{{7m - 2}}{{m + 1}} = 1$ to find the required value.

Complete step-by-step answer:
Let us assume that $m$ is the ratio in which $i + 2j + 3k$ divides the join of $- 2i + 3j + 5k$ and $7i - k$.
We are given that the $i + 2j + 3k$ divides the join of $- 2i + 3j + 5k$ and $7i - k$.
We will first find the coordinates for the given equations, $i + 2j + 3k$, $- 2i + 3j + 5k$ and $7i - k$.
We have,
$\left( {1,2,3} \right)$
$\left( { - 2,3,5} \right)$
$\left( {7,0, - 1} \right)$
Plotting the above points on the line, we get

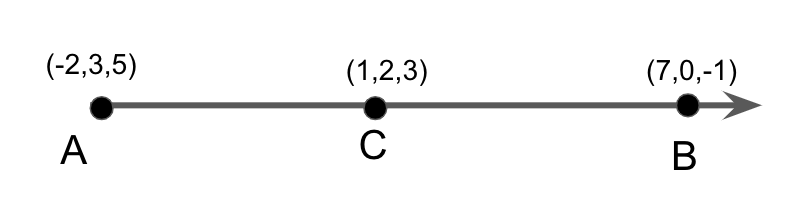
Now equating the three points A, B and C, we get
$\Rightarrow \dfrac{{7m - 2}}{{m + 1}} = 1$
Cross-multiplying the above equation, we get
$\Rightarrow 7m - 2 = m + 1$
Subtracting the above equation by $m$ on both sides, we get

$$\Rightarrow 7m - 2 - m = m + 1 - m \\\ \Rightarrow 6m - 2 = 1 \\\$$

Adding the above equation by 2 on both sides, we get

$$\Rightarrow 6m - 2 + 2 = 1 + 2 \\\ \Rightarrow 6m = 3 \\\$$

Dividing the above equation by 6 on both sides, we get

$$\Rightarrow \dfrac{{6m}}{6} = \dfrac{3}{6} \\\ \Rightarrow m = \dfrac{1}{2} \\\$$

Hence, the required ratio is $1:2$.
Thus, option B is correct.

Note: In solving these types of questions, students should make diagrams for better understanding and label the vertices properly to avoid confusion. One should know that the ratio is a way how much of one thing there is compared to another thing.