Question

The ratio $\frac{2^{\log_{2^{1/4}} a} - 3^{\log_{27} (a^2+1)^3} - 2a}{7^{4\log_{49} a} - a - 1}$ simplifies to :

• A. $a^2 - a - 1$
• B. $a^2 + a - 1$
• C. $a^2 - a +$

Answer 1

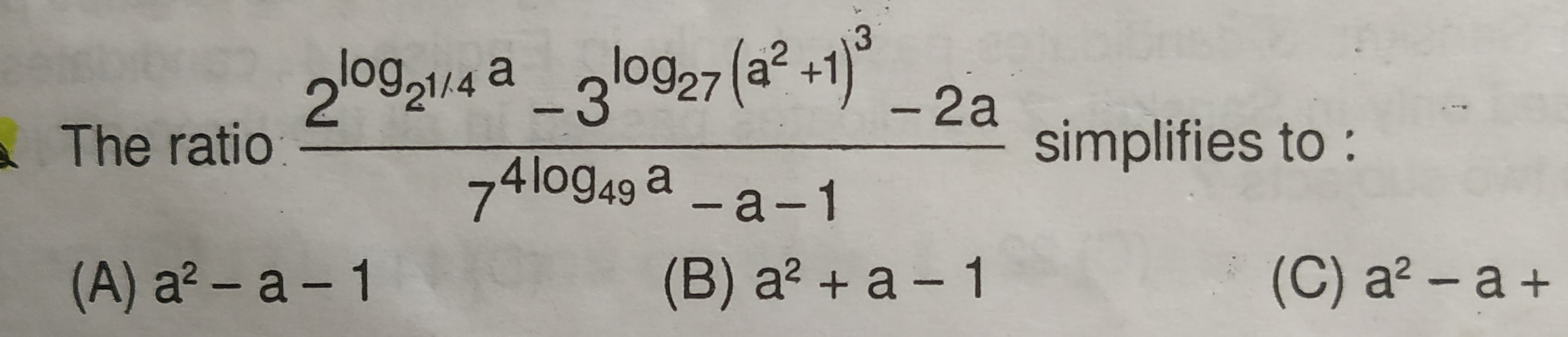
$a^2 + a + 1$ (assuming option C is a typo and should be $a^2 + a + 1$)

Answer 2

The given expression is $\frac{2^{\log_{2^{1/4}} a} - 3^{\log_{27} (a^2+1)^3} - 2a}{7^{4\log_{49} a} - a - 1}$.

First, simplify the terms in the numerator:

Term 1: $2^{\log_{2^{1/4}} a}$

Using the property $\log_{b^k} x = \frac{1}{k} \log_b x$, we have $\log_{2^{1/4}} a = \frac{1}{1/4} \log_2 a = 4 \log_2 a$.

So, $2^{\log_{2^{1/4}} a} = 2^{4 \log_2 a} = 2^{\log_2 a^4}$.

Using the property $b^{\log_b x} = x$, we get $2^{\log_2 a^4} = a^4$.

Term 2: $3^{\log_{27} (a^2+1)^3}$

Using the property $\log_{b^k} x = \frac{1}{k} \log_b x$, we have $\log_{27} (a^2+1)^3 = \log_{3^3} (a^2+1)^3 = \frac{1}{3} \log_3 (a^2+1)^3$.

Using the property $\log_b x^m = m \log_b x$, we get $\frac{1}{3} \cdot 3 \log_3 (a^2+1) = \log_3 (a^2+1)$.

So, $3^{\log_{27} (a^2+1)^3} = 3^{\log_3 (a^2+1)}$.

Using the property $b^{\log_b x} = x$, we get $3^{\log_3 (a^2+1)} = a^2+1$.

The numerator is $a^4 - (a^2+1) - 2a = a^4 - a^2 - 1 - 2a$.

Now, simplify the terms in the denominator:

Term 1: $7^{4\log_{49} a}$

Using the property $m \log_b x = \log_b x^m$, we have $4\log_{49} a = \log_{49} a^4$.

Using the property $\log_{b^k} x = \frac{1}{k} \log_b x$, we have $\log_{49} a^4 = \log_{7^2} a^4 = \frac{1}{2} \log_7 a^4$.

Using the property $\log_b x^m = m \log_b x$, we get $\frac{1}{2} \cdot 4 \log_7 a = 2 \log_7 a = \log_7 a^2$.

So, $7^{4\log_{49} a} = 7^{\log_7 a^2}$.

Using the property $b^{\log_b x} = x$, we get $7^{\log_7 a^2} = a^2$.

The denominator is $a^2 - a - 1$.

The expression simplifies to $\frac{a^4 - a^2 - 2a - 1}{a^2 - a - 1}$.

Let's perform polynomial division of the numerator by the denominator. Consider the division $(a^4 - a^2 - 2a - 1) \div (a^2 - a - 1)$. We can observe or perform long division that: $a^4 - a^2 - 2a - 1 = a^4 - a^3 - a^2 + a^3 - a^2 - a + a^2 - a - 1$ $= a^2(a^2 - a - 1) + a(a^2 - a - 1) + 1(a^2 - a - 1)$ $= (a^2 - a - 1)(a^2 + a + 1)$.

So the expression becomes $\frac{(a^2 - a - 1)(a^2 + a + 1)}{a^2 - a - 1}$. Assuming $a^2 - a - 1 \neq 0$, we can cancel the term $(a^2 - a - 1)$. The simplified expression is $a^2 + a + 1$.