Question

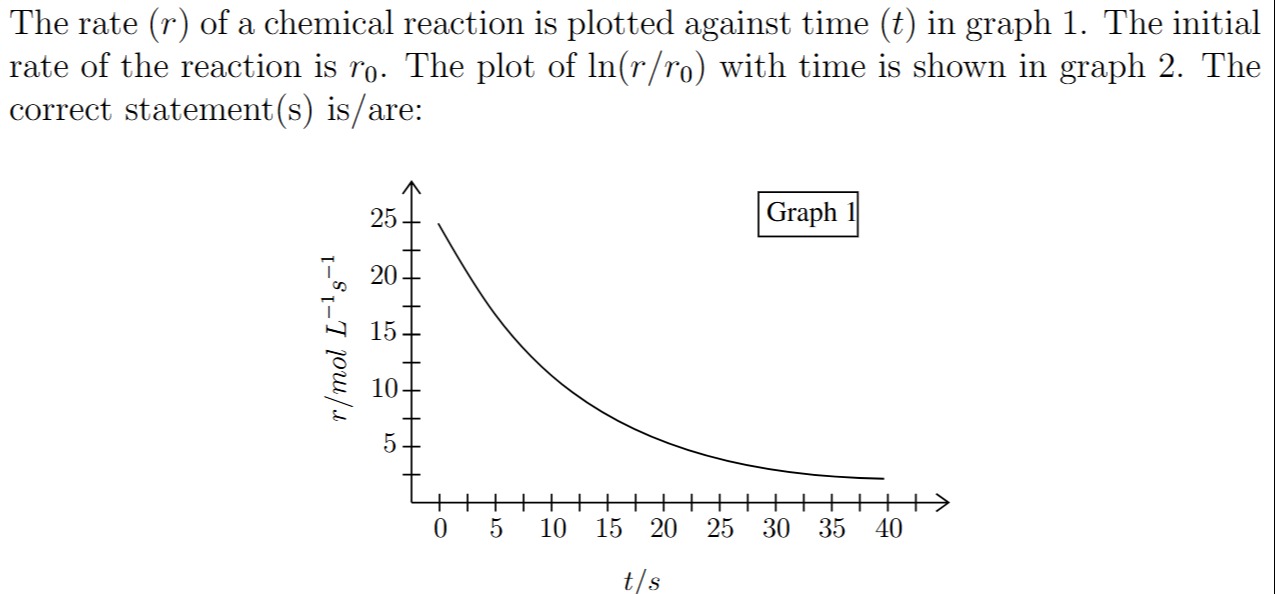
The rate $(r)$ of a chemical reaction is plotted against time $(t)$ in graph 1. The initial rate of the reaction is $r_0$. The plot of $\ln(r/r_0)$ with time is shown in graph 2. The correct statement(s) is/are:

Answer 1

The reaction is a first-order reaction. Graph 2 is a straight line with a negative slope. The rate constant is approximately $0.0924 \ s^{-1}$. The half-life is approximately $7.5 \ s$.

Answer 2

The problem provides Graph 1, which plots the rate ($r$) of a chemical reaction against time ($t$). It also states that Graph 2 shows a plot of $\ln(r/r_0)$ against time, where $r_0$ is the initial rate. We need to identify the correct statement(s) about the reaction based on these graphs.

Analysis of Graph 1:

1. Initial Rate ($r_0$): From Graph 1, at $t=0$, the rate $r_0 \approx 24 \text{ mol L}^{-1} \text{s}^{-1}$.
2. Rate Change with Time: The graph shows that the rate of the reaction decreases exponentially with time. This type of decay is characteristic of a first-order reaction.

Theoretical Background for Reaction Orders: For a general reaction $A \rightarrow \text{products}$, the rate is given by $r = k[A]^n$, where $n$ is the order of the reaction.

• Zero-order reaction ($n=0$): $r = k$. The rate is constant and independent of concentration. A plot of $r$ vs $t$ would be a horizontal line. This contradicts Graph 1.
• First-order reaction ($n=1$): $r = k[A]$. The rate is directly proportional to the concentration of the reactant. The integrated rate law is $\ln[A]_t = \ln[A]_0 - kt$. Since $r = k[A]$, we can write $[A] = r/k$. Substituting this into the integrated rate law: $$\ln\left(\frac{r_t}{k}\right) = \ln\left(\frac{r_0}{k}\right) - kt$$ $$\ln r_t - \ln k = \ln r_0 - \ln k - kt$$ $$\ln r_t = \ln r_0 - kt$$ Rearranging this equation, we get: $$\ln\left(\frac{r_t}{r_0}\right) = -kt$$ This equation shows that for a first-order reaction, a plot of $\ln(r/r_0)$ versus time ($t$) should yield a straight line with a negative slope equal to $-k$ and an intercept of 0 (since at $t=0$, $\ln(r_0/r_0) = \ln(1) = 0$).
• Second-order reaction ($n=2$): $r = k[A]^2$. The integrated rate law is $1/[A]_t = 1/[A]_0 + kt$. This does not lead to a linear relationship for $\ln(r/r_0)$ vs $t$.

Conclusion from Graph 1 and Theoretical Analysis: The exponential decay of rate observed in Graph 1 strongly suggests that the reaction is first-order. Consequently, Graph 2 (a plot of $\ln(r/r_0)$ vs $t$) must be a straight line with a negative slope.

Calculation of Rate Constant (k) and Half-life (t₁/₂): Since the reaction is first-order, we can use the relationship $\ln(r/r_0) = -kt$. We can pick two points from Graph 1 to determine the rate constant $k$.

Let's use the initial point and a point where the rate has clearly decreased. From Graph 1:

• At $t=0 \text{ s}$, $r_0 = 24 \text{ mol L}^{-1} \text{s}^{-1}$.
• At $t=15 \text{ s}$, $r = 6 \text{ mol L}^{-1} \text{s}^{-1}$.

Substitute these values into the first-order integrated rate law:

$$\ln\left(\frac{r}{r_0}\right) = -kt$$ $$\ln\left(\frac{6}{24}\right) = -k \times 15$$ $$\ln(0.25) = -15k$$ $$-1.386 = -15k$$ $$k = \frac{1.386}{15} \approx 0.0924 \text{ s}^{-1}$$

Let's verify with another point, for example, at $t=30 \text{ s}$, $r = 1.5 \text{ mol L}^{-1} \text{s}^{-1}$.

$$\ln\left(\frac{1.5}{24}\right) = -k \times 30$$ $$\ln(0.0625) = -30k$$ $$-2.772 = -30k$$ $$k = \frac{2.772}{30} \approx 0.0924 \text{ s}^{-1}$$

The rate constant $k$ is consistently approximately $0.0924 \text{ s}^{-1}$.

For a first-order reaction, the half-life ($t_{1/2}$) is given by:

$$t_{1/2} = \frac{\ln(2)}{k}$$ $$t_{1/2} = \frac{0.693}{0.0924 \text{ s}^{-1}} \approx 7.5 \text{ s}$$

We can also verify the half-life from Graph 1 directly:

• Initial rate $r_0 = 24 \text{ mol L}^{-1} \text{s}^{-1}$.
• Half of the initial rate is $24/2 = 12 \text{ mol L}^{-1} \text{s}^{-1}$.
• From Graph 1, the time at which $r=12 \text{ mol L}^{-1} \text{s}^{-1}$ is approximately $t=7.5 \text{ s}$. This matches our calculated half-life.

Correct Statements: Based on the analysis, the correct statements are:

1. The reaction is a first-order reaction.
2. Graph 2 (the plot of $\ln(r/r_0)$ with time) is a straight line.
3. The slope of Graph 2 is negative.
4. The rate constant ($k$) of the reaction is approximately $0.0924 \text{ s}^{-1}$.
5. The half-life ($t_{1/2}$) of the reaction is approximately $7.5 \text{ s}$.

The question asks for the correct statement(s) but does not provide options. Assuming typical options for such a question, the fundamental conclusions are the order of the reaction and properties derived from it.