Question

The rate of reaction generally doubles for each ${10^ \circ }$ rise in temperature. Explain it on the basis of Maxwell distribution of energies of molecules.

Answer 1

Maxwell-Boltzmann distribution law: It states that the probability of finding a fraction of molecules of a gas is a function of its mass, velocity and temperature. It is used to determine the velocity of molecules at a certain set of conditions.

Complete answer:
We know that it is impossible to calculate velocity of each molecule of a gas at every instant. Therefore, we use Maxwell Boltzmann distribution law to determine the velocity of molecules at a particular instant of time. The expression for this law is given as follows:
$\dfrac{{dN}}{N} = {\left( {\dfrac{m}{{2\pi {k_B}T}}} \right)^{\dfrac{1}{2}}}{e^{\left( {\dfrac{{ - m{v^2}}}{{2{k_B}T}}} \right)}}dv$
Where,
$\dfrac{{dN}}{N} \Rightarrow$ Fraction of molecules moving from velocity $v$ to $v + dv$
$m \Rightarrow$mass of the given molecule $T \Rightarrow$ Temperature of the molecule
${k_B} \Rightarrow$Boltzmann constant
The graph for Maxwell Boltzmann distribution law is plotted as follows: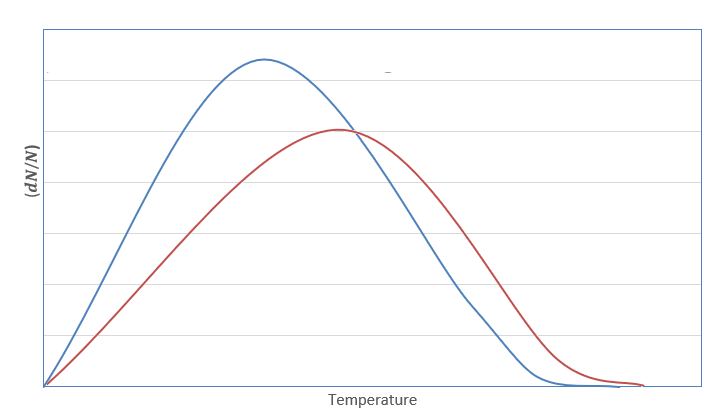
Here, the blue curve represents velocity at temperature ${T_1}$ whereas the red curve represents velocity at temperature ${T_2}$. The area under the curve is a fraction of molecules present.
As we can see for the given curve ${T_2} > {T_1}$ , and the area under the curve decreases i.e., fraction of molecules decreases on increasing temperature.
Therefore, according to Maxwell Boltzmann law, when temperature is increased, the fraction of molecules decreases. So, the activation energy required to convert the molecules into product will also be decreased.
Hence, according to the Arrhenius equation, a decrease in the value of activation energy will increase the rate of reaction.

Note:
Arrhenius equation: It states that the rate constant of reaction is a function of activation energy and temperature. It is expressed as $k = A{e^{\left( {\dfrac{{ - {E_a}}}{{RT}}} \right)}}$. As the rate constant is the negative exponential function of activation energy that means on increasing the value of activation energy, the value of rate constant decreases.