Question

The rate constants for decomposition of acetaldehyde have been measured over the temperature range 700-1000 K.

The data has been analysed by plotting $\ln k$ vs $\frac{10^3}{T}$ graph. The value of activation energy for the reaction is ______ kJ mol$^{-1}$. (Nearest integer) (Given : R = 8.31 J K$^{-1}$ mol$^{-1}$)

Answer 1

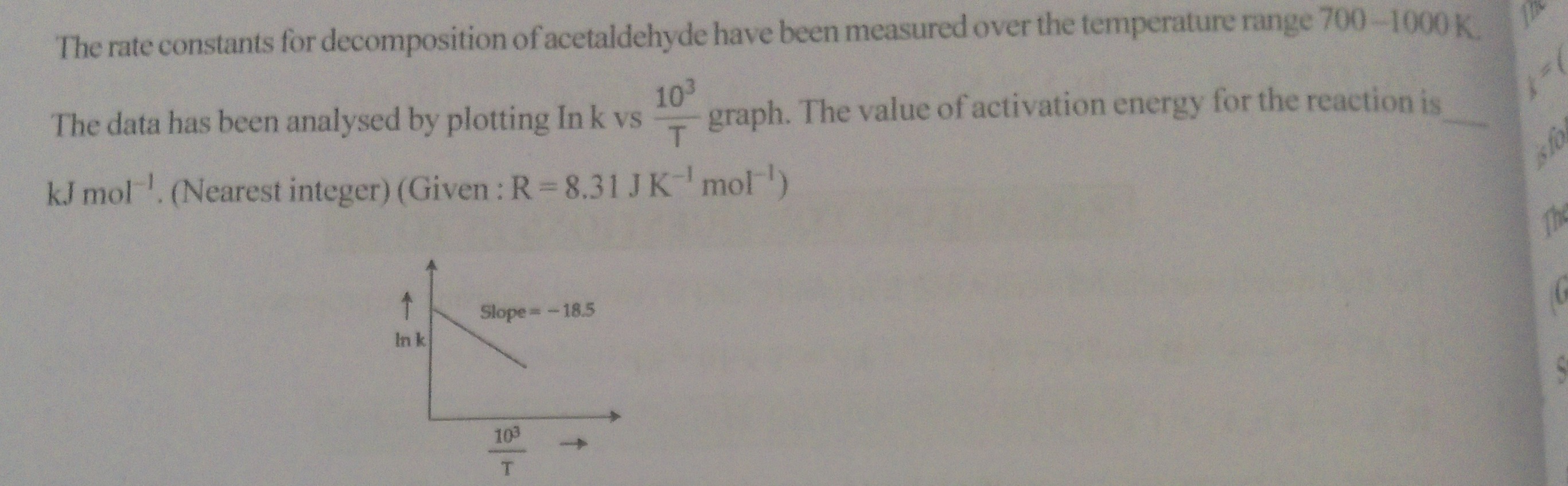
154 kJ mol$^{-1}$

Answer 2

The Arrhenius equation in linear form is:

$\ln k = \ln A - \frac{E_a}{RT}$

When plotted as $\ln k$ vs. $\frac{10^3}{T}$, note that:

$\frac{1}{T} = \frac{1}{10^3} \left(\frac{10^3}{T}\right)$

Thus the equation becomes:

$\ln k = \ln A - \frac{E_a}{R} \cdot \frac{1}{10^3}\left(\frac{10^3}{T}\right)$

which is of the form $\ln k = \text{constant} + \left[-\frac{E_a}{10^3 R}\right]\left(\frac{10^3}{T}\right)$.

Given that the slope of this plot is $-18.5$, we have:

$-\frac{E_a}{10^3 R} = -18.5 \quad \Longrightarrow \quad \frac{E_a}{10^3 R} = 18.5$

Solving for $E_a$:

$E_a = 18.5 \times 10^3 \times R$

With $R = 8.31\, \text{J}\,\text{K}^{-1}\,\text{mol}^{-1}$,

$E_a = 18.5 \times 10^3 \times 8.31 \, \text{J mol}^{-1} \approx 153735 \, \text{J mol}^{-1}$

Converting to kJ mol$^{-1}$:

$E_a \approx 153.7\, \text{kJ mol}^{-1} \approx 154\, \text{kJ mol}^{-1}\quad (\text{nearest integer})$.