Question
Question: The range of the function $f(x) = \sqrt{4-x^2} + \sqrt{x^2-1}$ is...
The range of the function f(x)=4−x2+x2−1 is
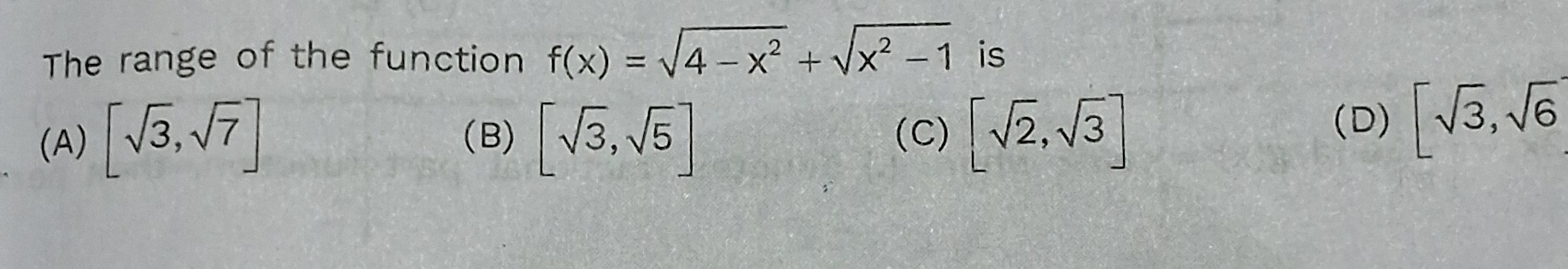
A
[3,7]
B
[3,5]
C
[2,3]
D
[3,6]
Answer
[3,6]
Explanation
Solution
To find the range of the function f(x)=4−x2+x2−1, we follow these steps:
-
Determine the domain:
We need 4−x2≥0 and x2−1≥0. This implies −2≤x≤2 and (x≤−1 or x≥1). Thus, the domain is [−2,−1]∪[1,2]. -
Substitute u=x2:
As x varies over the domain, u varies over [1,4]. The function becomes g(u)=4−u+u−1. -
Find the range of g(u):
We analyze g(u) on the interval [1,4].- Evaluate at endpoints: g(1)=3 and g(4)=3.
- Find critical points: g′(u)=24−u−1+2u−11. Setting g′(u)=0, we get u=25.
- Evaluate at the critical point: g(25)=4−25+25−1=23+23=223=6.
-
Compare values:
We have g(1)=3, g(4)=3, and g(25)=6. -
Determine the range:
The minimum value is 3 and the maximum value is 6. Therefore, the range of f(x) is [3,6].
