Question
Question: The range of a ∈ R for which the function $f(x) = (4a - 3)(x + \log_e 5)+2(a - 7)\cot(\frac{x}{2})\s...
The range of a ∈ R for which the function f(x)=(4a−3)(x+loge5)+2(a−7)cot(2x)sin2(2x), x=2nπ,n∈N, has critical points, is:
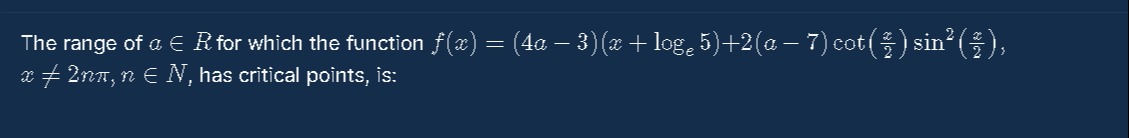
[-4/3, 2]
Solution
The function is f(x)=(4a−3)(x+loge5)+(a−7)sin(x). The derivative is f′(x)=(4a−3)+(a−7)cos(x). Critical points exist if f′(x)=0 has a solution. If a=7, f′(x)=25, which is never zero. If a=7, then cos(x)=−a−74a−3=a−73−4a. For a solution to exist, we need −1≤a−73−4a≤1. Solving a−73−4a≤1 gives a−710−5a≤0⟹a−7a−2≥0, so a∈(−∞,2]∪(7,∞). Solving a−73−4a≥−1 gives a−7−3a−4≥0⟹a−73a+4≤0, so a∈[−4/3,7). The intersection of these ranges is a∈[−4/3,2]. We need to ensure that the solutions x are in the domain x=2nπ. If a=2, cos(x)=1, so x=2kπ. x=0 is a solution in the domain. If a=−4/3, cos(x)=−1, so x=(2k+1)π. These are not of the form 2nπ. For a∈(−4/3,2), cos(x)∈(−1,1), so x=2kπ. Thus, the range of a is [−4/3,2].
