Question

The radius of the circle passing through the centre of the in-circle of ∆ABC and through the end points of BC is given by

• A. cos A
• B. $\frac { \mathrm { a } } { 2 }$ sec A/2
• C. sin A
• D. a sec A/2

Answer 1

Answer: (B)

$\frac { \mathrm { a } } { 2 }$ sec A/2

Answer 2

Q ∠BIC = 180⁰ –

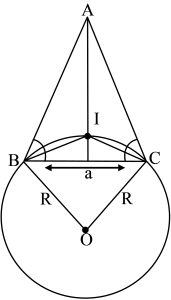
So ∠BOC = 2

= 360⁰ – (B + C)

= 180⁰ – A {∴ A + B + C = 180⁰)

= π – A

In ∆OBC

cos (π – A) =

⇒ a² = 2R² (1 + cos A)

R = = $\frac { \mathrm { a } } { 2 }$ sec $\frac { \mathrm { A } } { 2 }$