Question

The radius of the circle of least size that passes through (– 2, 1) and touches both axes is?
(a) 1
(b) 2
(c) 3
(d) 5

Answer 1

Hint: Assume the center of the circle with two variables. By using the given point, find the quadrant in which the circle lies. Now, try to get a relation between two variables using the condition given. Apply the equation of the circle and then substitute this point to find the variables. From these variables, find the value of the radius of the circle which is our required result.

Complete step-by-step answer:
Let us assume the center of the circle is (a, b). So, we get, center = (a, b).
The point given through which our circle passes is written as (– 2, 1)
The x – coordinate of this point is a negative value and the y – coordinate of the same point is a positive value. By the above condition, we can say the point is in the second quadrant. The given condition on the circle is that it touches both the axes. So, the circle must lie in the second quadrant. So, the circle must lie on the axes as a negative x-axis, positive y-axis.

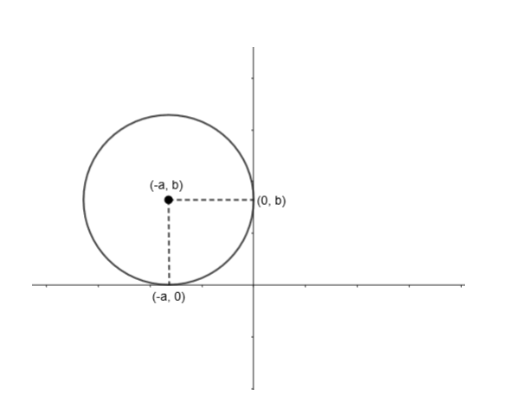
The center is now (– a, b) as it is in the second quadrant. Now, by dropping the perpendicular to axes, we get the point (0, b), (– a, 0) passing through the circle. As the radius of the circle is equal we can say a = b from the diagram. Now, we can write the center as (– a, a). So, we need a circle of radius and a center is (– a, a).
We know the equation of the circle of center (g, h) with radius r is:
${{\left( x-g \right)}^{2}}+{{\left( y-h \right)}^{2}}={{r}^{2}}$
By applying this here, we can write the equation as:
${{\left( x+a \right)}^{2}}+{{\left( y-a \right)}^{2}}={{a}^{2}}$
It is given that the circle passes through (– 2, 1), so we can say:
${{\left( -2+a \right)}^{2}}+{{\left( 1-a \right)}^{2}}={{a}^{2}}$
By simplifying, we can write the equation as,
${{\left( a-1 \right)}^{2}}+{{\left( a-2 \right)}^{2}}={{a}^{2}}$
By using ${{\left( a-b \right)}^{2}}={{a}^{2}}+{{b}^{2}}-2ab,$ we can expand our equation as:
${{a}^{2}}+1-2a+{{a}^{2}}+4-4a={{a}^{2}}$
By grouping the terms together after subtracting ${{a}^{2}}$ on both the sides, we get,
$\left( {{a}^{2}}+{{a}^{2}}-{{a}^{2}} \right)+\left( -2a-4a \right)+\left( 1+4 \right)={{a}^{2}}-{{a}^{2}}$
By simplifying the above equation, we get,
${{a}^{2}}-6a+5=0$
By writing 6a as – 5a – a and taking a common from the first two terms, we get,
$a\left( a-5 \right)-a+5=0$
By taking (a – 5) term common, we can write the equation as:
$\left( a-5 \right)\left( a-1 \right)=0$
So, the roots of the equation can be written in the form of:
a = 5 or a = 1
Given, we need the least size of the circle. So, we get the root as a = 1 as the radius.
Therefore option (a) is the right answer.

Note: The idea of keeping the circle in the second quadrant by using the point given is very important. Don’t forget to substitute the value of the radius also in terms of the variable or else you will not be able to solve for the value of the radius. Substitute the point carefully, if you misplace the values, the whole answer might go wrong.