Question

The radius of the circle in which the sphere ${x^2} + {y^2} + {z^2} + 2x - 2y - 4z - 19 = 0$ is cut by the plane $x + 2y + 2z + 7 = 0$ is
A. $2$
B. $3$
C. $4$
D. $1$

Answer 1

We draw the diagram of a sphere which is cut by a plane, which will give us a circle at that place. Comparing the general equation of sphere to the given equation of sphere we find the center of sphere and radius of sphere. Then we find the distance from the center of the sphere to the plane using the formula of shortest distance from a point to the plane. Applying Pythagoras theorem in the triangle formed by radius of sphere, radius of circle and the distance from point to the plane we find the radius of the circle.

• General equation of a Sphere is ${(x - a)^2} + {(y - b)^2} + {(z - c)^2} = {r^2}$
• Shortest distance between a point $P({x_1},{y_1},{z_1})$to the plane $Ax + By + Cz + D = 0$is given by $d = \dfrac{{\left| {A{x_1} + B{y_1} + C{z_1} + D} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}$
• Pythagoras theorem states that in a right angled triangle, square of hypotenuse is equal to sum of square of base and square of perpendicular.

Complete step-by-step answer:
We draw a sphere ${x^2} + {y^2} + {z^2} - 2z - 2y - 4z - 19 = 0$ which is cut by a plane $x + 2y + 2z + 7 = 0$.

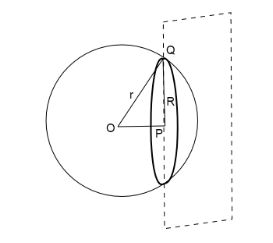
Here the radius of the sphere is r and the radius of the circle is R. The plane cuts the sphere of radius r and at that place of cut a circle of radius R is formed. $OP \bot PQ$.
The general equation of a sphere is ${(x - a)^2} + {(y - b)^2} + {(z - c)^2} = {r^2}$.
We are given the equation of the sphere is ${x^2} + {y^2} + {z^2} - 2z - 2y - 4z - 19 = 0$.
We can write the equation by shifting the constant to opposite side as ${x^2} + {y^2} + {z^2} - 2z - 2y - 4z = 19$
We transform the given equation of the sphere by adding constants to both sides of the equation.
We have ${x^2} + {y^2} + {z^2} + 2z - 2y - 4z = 19$ … (1)
Write the values of x together, y together and z together.
$\Rightarrow {x^2} + 2x + {y^2} - 2y + {z^2} - 4z - 19 = 0$
Add 1 along with values of variable x, add along the values of variable y and add 4 along the values of variable z and add all the three values on RHS as well.
$\Rightarrow {x^2} + 2x + 1 + {y^2} - 2y + 1 + {z^2} - 4z + 4 = 19 + 1 + 1 + 4$
Write $1 = {1^2},4 = {2^2}$
$\Rightarrow ({x^2} + 2x + {1^2}) + ({y^2} - 2y + {1^2}) + ({z^2} - 4z + {2^2}) = 25$
We know ${(a + b)^2} = {a^2} + {b^2} + 2ab,{(a - b)^2} = {a^2} + {b^2} - 2ab$
Therefore we can write
$\Rightarrow {(x + 1)^2} + {(y - 1)^2} + {(z - 2)^2} = 25$
Now we can write RHS of the equation as $25 = {5^2}$
$\Rightarrow {(x + 1)^2} + {(y - 1)^2} + {(z - 2)^2} = {5^2}$
$\Rightarrow {(x - ( - 1))^2} + {(y - 1)^2} + {(z - 2)^2} = {5^2}$
Now comparing with the general equation of sphere ${(x - a)^2} + {(y - b)^2} + {(z - c)^2} = {r^2}$
$a = - 1,b = 1,c = 2,r = 5$
Therefore, the sphere has radius $(a,b,c) = ( - 1,1,2)$ and radius of sphere is 5.
Now we calculate the shortest distance from the point $O( - 1,1,2)$ to plane $x + 2y + 2z + 7 = 0$.
We know the shortest distance between a point $P({x_1},{y_1},{z_1})$ to the plane $Ax + By + Cz + D = 0$ is given by $d = \dfrac{{\left| {A{x_1} + B{y_1} + C{z_1} + D} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}$
Substituting the values of ${x_1} = - 1,{y_1} = 1,{z_1} = 2,A = 1,B = 2,C = 2,D = 7$
$\Rightarrow d = \dfrac{{\left| {(1)( - 1) + (2)(1) + (2)(2) + 7} \right|}}{{\sqrt {{{(1)}^2} + {{(2)}^2} + {{(2)}^2}} }}$
$\Rightarrow d = \dfrac{{\left| { - 1 + 2 + 4 + 7} \right|}}{{\sqrt {1 + 4 + 4} }}$
$\Rightarrow d = \dfrac{{\left| {12} \right|}}{{\sqrt 9 }}$
Writing the value of $9 = {3^2}$
$\Rightarrow d = \dfrac{{12}}{{\sqrt {{3^2}} }}$
Cancel square root by square power
$\Rightarrow d = \dfrac{{12}}{3}$
Cancel the same factors from numerator and denominator.
$\Rightarrow d = 4$
Therefore, $OP = 4$
Therefore, in $\vartriangle OPQ$, $\angle P = {90^ \circ }$, $OP = 4$, $OQ = 5$
In the right triangle we can apply Pythagoras theorem.
$\Rightarrow O{P^2} + P{Q^2} = O{Q^2}$
Substituting the values we get
$\Rightarrow {(4)^2} + P{Q^2} = {(5)^2}$
Calculating the squares
$\Rightarrow 16 + P{Q^2} = 25$
Shift all constants to one side of the equation

$$\Rightarrow P{Q^2} = 25 - 16 \\\ \Rightarrow P{Q^2} = 9 \\\$$

Write the term in RHS as square of a number
$\Rightarrow P{Q^2} = {3^2}$
Take square root on both sides of the equation
$\Rightarrow \sqrt {P{Q^2}} = \sqrt {{3^2}}$
Cancel square root by square power
$\Rightarrow PQ = 3$
Therefore, the radius of the circle is 3 units.

So, option B is correct.

Note: Students are likely to make mistakes when they forcefully compare the equation of sphere directly to the general equation of sphere which is wrong and technically cannot be done. Also, keep in mind the hypotenuse of a right angled triangle is always the side that is opposite to the right angle of the triangle, so while applying Pythagoras theorem always write hypotenuse on one side of the equation and base and perpendicular on the other side.