Question

The radius of gyration of a plane lamina of mass M, length L and breadth B about an axis passing through its centre of gravity and perpendicular to its plane will be
$\begin{aligned} & \text{A}\text{. }\sqrt{\dfrac{\left( {{L}^{2}}+{{B}^{2}} \right)}{12}} \\\ & \text{B}\text{. }\sqrt{\dfrac{\left( {{L}^{2}}+{{B}^{2}} \right)}{8}} \\\ & \text{C}\text{. }\sqrt{\dfrac{\left( {{L}^{2}}+{{B}^{2}} \right)}{2}} \\\ & \text{D}\text{. }\sqrt{\dfrac{\left( {{L}^{3}}+{{B}^{3}} \right)}{12}} \\\ \end{aligned}$

Answer 1

Obtain the mathematical expression for the radius of gyration in terms of the moment of inertia and the mass of the system. Find the moment of inertia of the system about an axis passing through the centre of gravity and perpendicular to the plane. Use this value in the expression for radius of gyration to find our answer.

Complete step by step answer:
The radius of gyration about an axis of rotation of a body can be defined as the radial distance to a point which will have the same moment of inertia if the total mass of the body were concentrated as the actual distribution of the mass of the body.
Moment of inertia of a body can be defined in terms of the radius of gyration as,
$I=m{{k}^{2}}$
Where, I is the moment of inertia, M is the mass and k is the radius of gyration.
So, we can write radius of gyration as,
$k=\sqrt{\dfrac{I}{m}}$
Let the area density of the lamina is $\rho$ .
$\rho =\dfrac{M}{LB}$
Moment of inertia of the lamina can be written as, $\int{\int{\rho {{r}^{2}}dA}}$
Where, r is the distance of each point to the axis of rotation and dA is the differential area.
Let, the centre of the rectangular lamina is (0,0). So the distance from a point (x,y) to the axis of rotation of the plane will be, ${{r}^{2}}={{x}^{2}}+{{y}^{2}}$ .

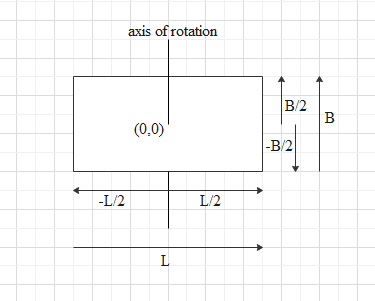
So, we can write

& I=\int\limits_{-\dfrac{L}{2}}^{\dfrac{L}{2}}{\int\limits_{-\dfrac{B}{2}}^{\dfrac{B}{2}}{\rho \left( {{x}^{2}}+{{y}^{2}} \right)dxdy}} \\\ & I=\int\limits_{-\dfrac{L}{2}}^{\dfrac{L}{2}}{\left[ \rho \left( {{x}^{2}}y+\dfrac{{{y}^{3}}}{3} \right) \right]_{-\dfrac{B}{2}}^{\dfrac{B}{2}}dx} \\\ & I=\int\limits_{-\dfrac{L}{2}}^{\dfrac{L}{2}}{\left[ \rho \left( {{x}^{2}}B+\dfrac{{{B}^{3}}}{12} \right) \right]dx} \\\ & I=\left[ \rho \left( \dfrac{{{x}^{3}}}{3}B+\dfrac{x{{B}^{3}}}{12} \right) \right]_{-\dfrac{L}{2}}^{\dfrac{L}{2}} \\\ & I=\rho \left( \dfrac{{{L}^{3}}B}{12}+\dfrac{L{{B}^{3}}}{12} \right) \\\ \end{aligned}$$ Putting the value of $\rho $ , $$\begin{aligned} & I=\dfrac{M}{LB}\left( \dfrac{{{L}^{3}}B}{12}+\dfrac{L{{B}^{3}}}{12} \right) \\\ & I=M\left( \dfrac{{{L}^{2}}}{12}+\dfrac{{{B}^{2}}}{12} \right) \\\ & I=M\left( \dfrac{{{L}^{2}}+{{B}^{2}}}{12} \right) \\\ \end{aligned}$$ So, we can express the radius of gyration f the plane lamina as, $\begin{aligned} & k=\sqrt{\dfrac{I}{M}} \\\ & k=\sqrt{\dfrac{{{L}^{2}}+{{B}^{2}}}{12}} \\\ \end{aligned}$ The correct option is (A). **Note:** The radius of gyration for a system of masses is not constant. It depends on the distribution of the masses of the system about the axis of rotation and on the axis of rotation. If the axis of rotation of a system changes, the radius of gyration for the system will also change.