Question
Question: The radius of curvature of the left and right surfaces of a concave lens of refractive index 1.5 10 ...
The radius of curvature of the left and right surfaces of a concave lens of refractive index 1.5 10 and 15. The refractive index of liquid in either side of the concave lens is 2. Find the equivalent focal length
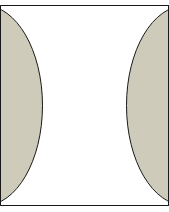
Solution
In this question, we will use the relation between focal length, refractive index and the given radii. Further, by substituting the given values, and solving we will get the required result. Also, we will discuss the basics of mirror, lens and types of lenses, for our better understanding.
Formula used:
f1=(μ−1)(R11−R21)
fe1=f11+f21+f31
Complete answer:
As we know, that we have a compound lens, the focal point is given as:
f11=(μ−1)(R11−R21)
Now, by substituting the given values in above equation, we get:
f11=(2−1)(∞1−−R1)
Further, solving we get:
f11=R1=101
Now, we have equation for the second focal length, which is given as:
f21=(μ−1)(R11−R21)
Now, by substituting the given values in above equation, we get
f21=(1.5−1)(101−151)
Further, solving we get:
f21=−0.5(1505)
⇒f2=−60
Similarly, we have equation for the second focal length, which is given as:
f31=(μ−1)(R21−R11)
Now, by substituting the given values in above equation, we get:
f31=(2−1)(R21−∞1)
⇒f31=R21=151
As we know, the equivalent focal length is given as:
fe1=f11+f21+f31
Now, substituting the values of focal length in above equation, we get:
fe1=101+−601+151
⇒fe1=609=203
∴fe=320cm
Therefore, we get the required answer, which gives us the value of equivalent focal length of the given concave lens.
Additional information:
As we know a mirror is defined as a device that contains a surface, which is mainly used to reflect light. As mirrors do not usually absorb much light, most of the light is redirected. The mirror and the object's overall quality is generally preserved in the new image.
In the given figure, the shaded portion is not used to reflect light.
convex mirror
concave mirror
Now, when we define a lens, we know that a lens is a transmissive optical device that focuses or disperses light beams by the means of refraction. For example- a lens can focus light to form an image, unlike a prism, which refracts light without focusing.
Here, there are two types of lenses, a simple lens and a compound lens. A simple lens consists of a single piece of transparent material. Compound lens consist of several simple lenses arranged along with a common axis
As we know that lenses are of two types.
This classification of lenses depends on how the light rays bend when they pass through the lens:
Convex Lens also called Converging lens:
Convex lenses are thick in the middle and thinner at the edges. . A convex lens is also known as the converging lens as the light rays bend inwards and converge at a point which is known as focal length.
Concave Lens also called Diverging lens:
Here, we define a concave lens which is flat in the middle and thicker at the edges. Also, a concave lens is known as a diverging lens as it bends the parallel light rays outward and diverges the light rays at the focal point.
Note: we should remember that a mirror will have only one focal point, which is in front of the mirror. Also, a lens has two focal points each on either side. We should note that compound lenses are constructed from a combination of different simple lenses. The lens which is used to build a compound lens may have different refractive indices and other properties.
