Question
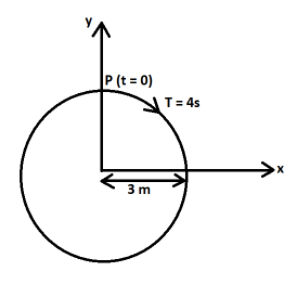
Question: The radius of circle, the period of revolution, initial position and sense of revolution are indicat...
The radius of circle, the period of revolution, initial position and sense of revolution are indicated in the fig., y- projection of the radius vector of rotating particle P is:
A.y(t)=−3cos2πt, where y in m
B.y(t)=4sin(2πt), where y in m
C.y(t)=3cos(23πt), where y in m
D.y(t)=3cos(2πt), where y in m
Solution
To find the y- projection of the radius vector of rotating particle P, can be deduced using the simple harmonic motion equation. The simple harmonic motion equation will be dependent on the type of function that you choose, i.e., sine or cosine, which can be deduced from the question.
Formula used:
ω=T2πy=acos(ωt)
Complete step by step answer:
Time-period (T) = 4s, is given in the question.
So,
ω=T2π
⇒ω=42π=2πrad/s
Now,
At t=0, y displacement is maximum, so the equation will be cosine function.
Hence,
y=acos(ωt), where a is the radius of the circle.
y=3cos(2πt)m
Therefore, the correct answer is Option (D).
Additional Information:
In mechanics and physics, simple harmonic motion is a special type of periodic motion where the restoring force on the moving object is directly proportional to the object's displacement magnitude and acts towards the object's equilibrium position. It results in an oscillation which, if uninhibited by friction or any other dissipation of energy, continues indefinitely.
Simple harmonic motion can serve as a mathematical model for a variety of motions, but is typified by the oscillation of a mass on a spring when it is subject to the linear elastic restoring force given by Hooke's law. The motion is sinusoidal in time and demonstrates a single resonant frequency. Other phenomena can be modeled by simple harmonic motion, including the motion of a simple pendulum, although for it to be an accurate model, the net force on the object at the end of the pendulum must be proportional to the displacement (and even so, it is only a good approximation when the angle of the swing is small; see small-angle approximation). Simple harmonic motion can also be used to model molecular vibration as well.
Note:
The important part in this question is to judge the type of function that needs to be used for getting the answer and to judge the type of periodic motion that is acting on this body. In this question, the type of periodic motion is Simple Harmonic Motion, which acts towards the equilibrium position for the body.
