Question

The radius of a circle with centre O is$7cm$. Two radii OA and OB are drawn at right angles to each other. Find the area of minor and major segments.

Answer 1

Any chord in the circle divides the circle into two parts. The bigger or the large part is known as the major segment, and the smaller one is known as the minor segment. We will use a formula to find the area of the minor segment first. Once we get the area of the minor segment, according to the property - we will need the find area of the major segment by subtracting the area of a minor segment from the area of a circle.

Complete step-by-step solution
The radius of the given circle is $7cm$ with centre O and, the two radii are perpendicular to each other in the same circle.

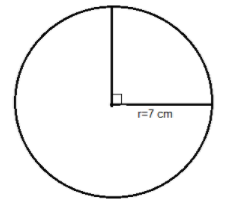
First, we find the area of the minor segment by using the formula $\left( {\dfrac{{\pi \theta }}{{360}} - \sin \dfrac{\theta }{2}\cos \dfrac{\theta }{2}} \right){r^2}$
Here, $\theta = {90^0}$ $r = 7cm$
${A_m} = \left( {\dfrac{{\pi \theta }}{{360}} - \sin {{45}^0}{{\cos }^0}} \right){7^2} \\\ = \left( {\dfrac{\pi }{4} - \dfrac{1}{4}} \right)49 \\\$
Substitute the value of $\pi = 3.14$ in the above equation, we get:
${A_m} = \left( {\dfrac{{3.14 - 1}}{4}} \right) \times 49 \\\ = \dfrac{{2.14}}{4} \times 49 \\\ = 0.535 \times 49 \\\ = 26.215c{m^2} \\\$
Now, the area of the major segment = area of the circle – area of the minor segment

$${A_M} = \pi {r^2} - 26.215 \\\ = 3.14{(7)^2} - 26.215 \\\ = 153.86 - 26.215 \\\ = 127.645{\text{ }}c{m^2} \\\$$

Hence, the required solution is the area of the minor segment is $26.25c{m^2}$, and the area of the major segment is $127.75c{m^2}$.

Note: In these types of problems where we need to find the area of the certain part which is connected with another part, we need to find the area of anyone part. Once we have an area of one part, another part can be calculated by subtracting the area calculated earlier from the total area of the shape. Always remember the basic properties of the segments.