Question
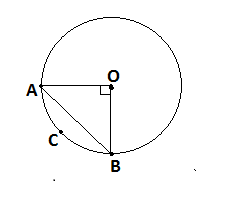
Question: The radius of a circle with centre O is 5 cm (given figure). Two radii OA and OB are drawn at right ...
The radius of a circle with centre O is 5 cm (given figure). Two radii OA and OB are drawn at right angles to each other. Find the areas of the segment made by the chord AB (Take π=3.14)
Solution
Hint: In this question, we use the concept of segment and sector of circle. To find the area of the segment , we have to find the area of the sector and the area of the triangle. We use the formula of area of sector =3600πr2θ, where θ is the angle subtended by chord at the center of circle and also area of right angle triangle is 21×(Base)×(Height).
Complete Step-by-Step solution:
Given, radius of circle, r=OA=OB=5cm and angle subtended by chord at the center of circle θ=900 .
Now, area of minor segment= (area of sector OACB)-(area of triangle OAB)
Area of sector OACB =3600πr2θ , where θ=900 and radius of circle, r=5cm
⇒3603.14×(5)2×90 ⇒43.14×25 ⇒478.5 ⇒19.62cm2
Area of sector OACB =19.62 cm2.
Now, we have to find the area of △OAB .
We can see △OAB is a right angle triangle so we use area of right angle triangle is 21×(Base)×(Height) where Base=5cm and Height=5cm
⇒21×5×5 ⇒225 ⇒12.5cm2
Area of minor segment = (area of sector OACB)-(area of triangle OAB)
⇒19.62−12.5 ⇒7.12cm2
Area of the minor segment made by the chord AB is 7.12 cm2.
Now, area of circle =πr2
⇒3.14×(5)2 ⇒78.5cm2
Area of major segment = Area of circle- Area of minor segment
Area of major segment =78.5-7.12=71.38
Area of the major segment made by chord AB is 71.38 cm2.
So, the area of minor and major segments made by chord AB is 7.12 cm2 and 71.38 cm2 respectively.
Note: In such types of problems first we find the area of minor sector and subtract the area of triangle from area of minor sector so we get area of minor segment and then find the area of circle and subtract area of minor segment from area of circle so we get the area of major segment.
