Question

The radius of a circle is $16cm$. The midpoint of a chord of the circle lies on the diameter perpendicular to the chord and its distance from the near end of the diameter is $3cm$. If the length of that chord is $m\sqrt {87} cm$, find the value of $m$.
A) 4
B) $8$
C) $2$
D) $1$

Answer 1

We can solve this problem using Pythagoras theorem. Since the diameter is perpendicular to the chord and bisects the chord, we can consider a right angled triangle. The hypotenuse will be the radius and other sides can be calculated with the given information.

Formula used:
Pythagoras theorem:
For a right angled triangle, ${\text{bas}}{{\text{e}}^{\text{2}}} + {\text{altitud}}{{\text{e}}^2} = {\text{hypotenuse}}{{\text{e}}^2}$, where hypotenuse is the side opposite to ${90^ \circ }$ angle.

Complete step-by-step answer:
Given that radius of the circle is $16cm$.
And also the midpoint of a chord of the circle lies on the diameter perpendicular to the chord.
So we can construct a right angled triangle.

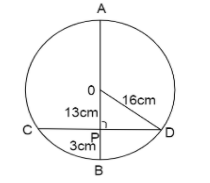
Here, $AB$ represents the diameter and $CD$ represents the chord perpendicular to it.
$\Rightarrow AB = 16 \times 2 = 32,CD = m\sqrt {87}$
So we have, $PC = PD$ (since diameter passes through the midpoint)
$OD$ is the radius of the circle gives $OD = 16cm$
$OB$ is also radius to the circle and $PB = 3cm$ (given)
So we have, $OP = OB - PB = 16cm - 3cm = 13cm$
Now $\vartriangle OPD$ is a right triangle with hypotenuse $OD$.
For a right angled triangle, ${\text{bas}}{{\text{e}}^{\text{2}}} + {\text{altitud}}{{\text{e}}^2} = {\text{hypotenuse}}{{\text{e}}^2}$, where hypotenuse is the side opposite to ${90^ \circ }$ angle.
So, we have, $O{P^2} + P{D^2} = O{D^2}$
$\Rightarrow P{D^2} = O{D^2} - O{P^2}$
Substituting the values we get,
$\Rightarrow P{D^2} = {16^2} - {13^2} = 256 - 169 = 87$
Taking square root on both sides we get,
$\Rightarrow PD = \sqrt {87} cm$
Since $PD$ is half the chord, length of the chord, $CD = 2\sqrt {87} cm$
But it is given that $CD = m\sqrt {87} cm$
Comparing we get, $m = 2$.
$\therefore$ The answer is option C.

Note: A diameter drawn perpendicular to any chord will bisect the chord. If as in the figure, $AB$ is the diameter and $CD$ is the chord perpendicular to it, then then $PC = PD$. Also we have $PA \times PB = P{C^2}$. Using this result too we can solve for $m$.