Question

The radius of a circle having minimum area, which touches the curve$y = 4 - {x^2}$ and the lines$y = \left| x \right|$ is.
A.$2\left( {\sqrt 2 + 1} \right)$
B.$2\left( {\sqrt 2 - 1} \right)$
C.$4\left( {\sqrt 2 - 1} \right)$
D.$4\left( {\sqrt 2 + 1} \right)$

Answer 1

Hint : In order to get a clear picture of the question in our mind we need to draw the curves $y = 4 - {x^2}$and $y = |x|$. But symmetry one can claim that the center of the required circle will lie on the y-axis. Then you need to use the formula for calculating length of perpendicular from center to the tangent $y = |x|$.

Complete step-by-step answer :
It is given that the radius of circle is minimum and it touches the curve $y = 4 - {x^2}$ and the lines, $y = |x|$
Let us draw $y = 4 - {x^2}\,\,and\,\,y = |x|$

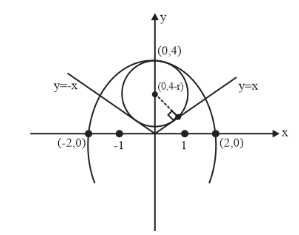
Let us assume that the radius of the circle is r. Then from figure it is clear that the center of the circle will be $\left( {0,4 - r} \right)$
Since $y = x$ is tangent to the circle, the line obtained by joining the center with the contact point will be perpendicular to the line $y = x$. The length of this perpendicular is equal to the radius of the circle.
We know that the length of perpendicular (d) drawn from point $\left( {\alpha ,\beta } \right)$ on the line $Ax + By + C = 0$ is given by
$d = \dfrac{{|A\alpha + B\beta + C|}}{{\sqrt {{A^2} + {B^2}} }}$
Hence, we have

$$\alpha = 0 \\\ \beta = 4 - r \\\ d = r \\\ \therefore r = \dfrac{{|0 - \left( {4 - r} \right) + 0|}}{{\sqrt {{1^2} + {{\left( { - 1} \right)}^2}} }} \\\ \Rightarrow r = \dfrac{{| - \left( {4 - r} \right)|}}{{\sqrt 2 }} \\\ \Rightarrow r = \dfrac{{|\left( {4 - r} \right)|}}{{\sqrt 2 }} \\\$$

From the figure, it is clear that radius r is less than 4. Therefore,

$$|4 - r| = 4 - r \\\ \therefore r = \dfrac{{4 - r}}{{\sqrt 2 }} \\\ \Rightarrow \sqrt 2 r + r = 4 \\\ \Rightarrow r = \dfrac{4}{{\sqrt 2 + 1}} \\\$$

Let is rationalize the number
$r = \dfrac{{4\left( {\sqrt 2 - 1} \right)}}{{\left( {\sqrt 2 + 1} \right)\left( {\sqrt 2 - 1} \right)}} = \dfrac{{4\left( {\sqrt 2 - 1} \right)}}{{2 - 1}} = 4\left( {\sqrt 2 - 1} \right)$
So, the correct answer is “Option C”.

Note : The students must be able to draw graphs of simple functions like straight line, quadratic polynomial, and modulus function. They must keep in mind the basic formulas of coordinate geometry such as distance between two parallel lines, length of perpendicular drawn from a point to a straight line. This reduces the complexity of the problems.