Question

The radii of two concentric circles are $16\,cm$ and $10\,cm$. $AB$ is the diameter of the bigger circle. $BD$ is the tangent to the smaller circle touching it at $D$ and intersecting the larger circle at P on produced. What is the length of $AP$?

Answer 1

Here we have two concentric circles of radii $16\,cm$ and $10\,cm$.Concentric circles are the circle with only one common centre. In order to solve this question we use the concept that any tangent on the circle from any point makes an angle $90^\circ$ with the radius of the circle and in any circle if the hypotenuse of the triangle is the diameter of the circle then the triangle inscribed in the circle is a right triangle.

Complete step by step answer:
This question can be represented by the following figure.

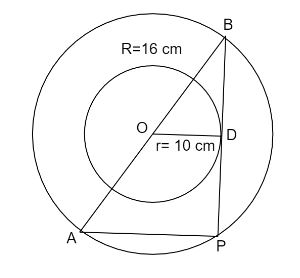
Let $O$ be the centre of the two concentric circles. The radii of the bigger circle is $16\,cm$ and the radii of the smaller circle is $10\,cm$. Therefore, $OB = R = 16\,cm$ and $OD = r = 10\,cm$. As $AB$ is the diameter of a bigger circle so it is equal to the double of the radius of the bigger circle. So $AB = D = R = 2R$. Put the value $R = 16\,cm$. We get the diameter of the bigger circle $AB = 32\,cm$. Now we know that any tangent on the circle from any point makes an angle $90^\circ$ with the radius of the circle.Therefore,
$\angle BDO = 90^\circ$

We have extended the tangent so that it intersects the bigger circle at point $P$, and joined the point $AP$ whose length is to be calculated.If the hypotenuse of the triangle is the diameter of the circle then the triangle inscribed in the circle is a right angle triangle.Let us consider the triangle $OBD$ and $ABP$. We have,
$\angle OBD = \angle ABP$ (Common)
$\Rightarrow \angle ODB = \angle APB = 90^\circ$
$\Rightarrow \angle DOB = \angle PAB$ (Alternate angle)
So, by $AAA$ congruence, these two triangles are congruent to each other.

We know that in a congruent triangle the ratio of the respective side is always equal. Therefore,
$\Rightarrow \dfrac{{OB}}{{AB}} = \dfrac{{OD}}{{AP}} = \dfrac{{DB}}{{PB}}$
So, $\dfrac{{OB}}{{AB}} = \dfrac{{OD}}{{AP}}$
Substituting the values in the above equation. We get,
$\Rightarrow \dfrac{{16}}{{32}} = \dfrac{{10}}{{AP}}$
Simplifying the above equation. We get,
$\Rightarrow \dfrac{1}{2} = \dfrac{{10}}{{AP}}$
$\therefore AP = 20\,cm$

Hence, the length of the $AP$ is $20\,cm$.

Note: These types of questions can also be solved using Pythagoras theorem in both the triangles as they are right angled triangles. According to Pythagoras theorem in a right triangle ${(Hypotenuse)^2} = {(Perpendicular)^2} + {(Base)^2}$. Concentric circles are the circles with only one common centre and the region between the concentric circles is called an Annulus. In concentric circles the longest chord of a circle is the diameter of the circle and radius that is drawn to the chord bisects the chord. A circle can be inscribed in square, triangle or a kite. An isosceles triangle is formed when the radii join the ends of a chord to the centre of a circle.