Question
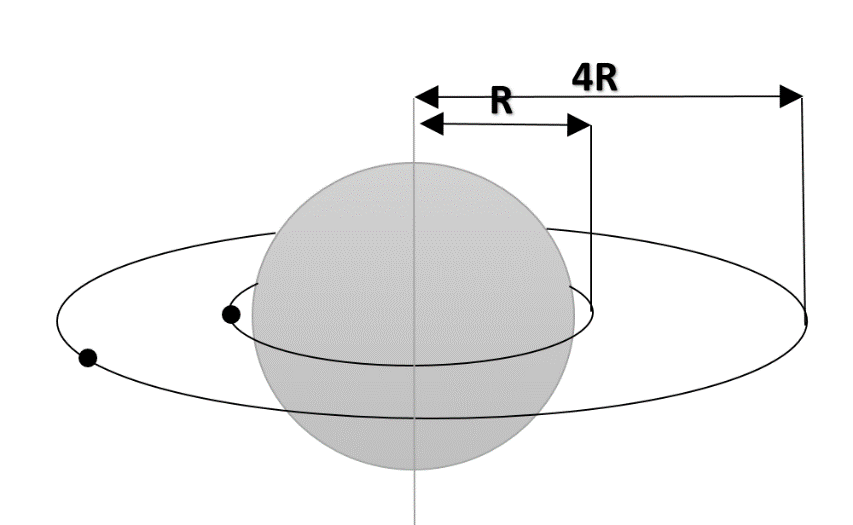
Question: The radii of orbit of two satellites A and B of earth are 4R and R respectively. If the speed of sat...
The radii of orbit of two satellites A and B of earth are 4R and R respectively. If the speed of satellite A is 3v, then the speed of satellite B will be:
A.43v
B.6v
C.12v
D.23v
Solution
When the satellite is launched in the orbit of earth, the only force acting on the satellite is gravity. Due to its launch motion, it starts revolving around earth and due to revolution, it experiences a centripetal force which is balanced by the gravitational force. This is the reason why a satellite remains stable in earth’s orbit without the fuel.
Formula used: Fcentripetal=rmv2, where ‘r’ is the radius of a rotating particle.
Complete step by step answer:
Let the radius of revolution of the satellite be ‘r’, measured from the centre of earth to its altitude. The centripetal force acting on the satellite isFcentripetal=rmv2.
This force acts radially outwards and the force of attraction of earth balances the centripetal force.
i.e. rmv2=r2GMm
Hence, v=rGMwhich is the orbital velocity of the satellite.
Since ‘G’ – gravitational constant and ‘M’ – mass of earth is same for both the satellites, hence we can write:
v2v1=r1r2
Or vBvA=rArB
Given that rB=R and rA=4R;
Hence rArB=41
Hence vBvA=rArB=41=21
Also given,vA=3v
Hence, vB=2×3v=6v
So, the correct answer is “Option B”.
Note: It is important to note that the velocity of a satellite does not depend upon the mass of the satellite itself. It is just dependent upon the distance of the satellite from the centre of earth. Hence two satellites at same orbit (means they have the same distance from centre of earth) will have the same velocity, irrespective of the mass. Infact even a lighter object like a meteor enters the orbit of a satellite, then both the object and the satellite will never collide. Hence it serves as an advantage and satellites remain safe.
