Question

The quarter disc of radius $R$ (see figure) has a uniform surface charge density $\sigma$.

Find electric potential at a point $(O, O, Z)$.

Answer 1

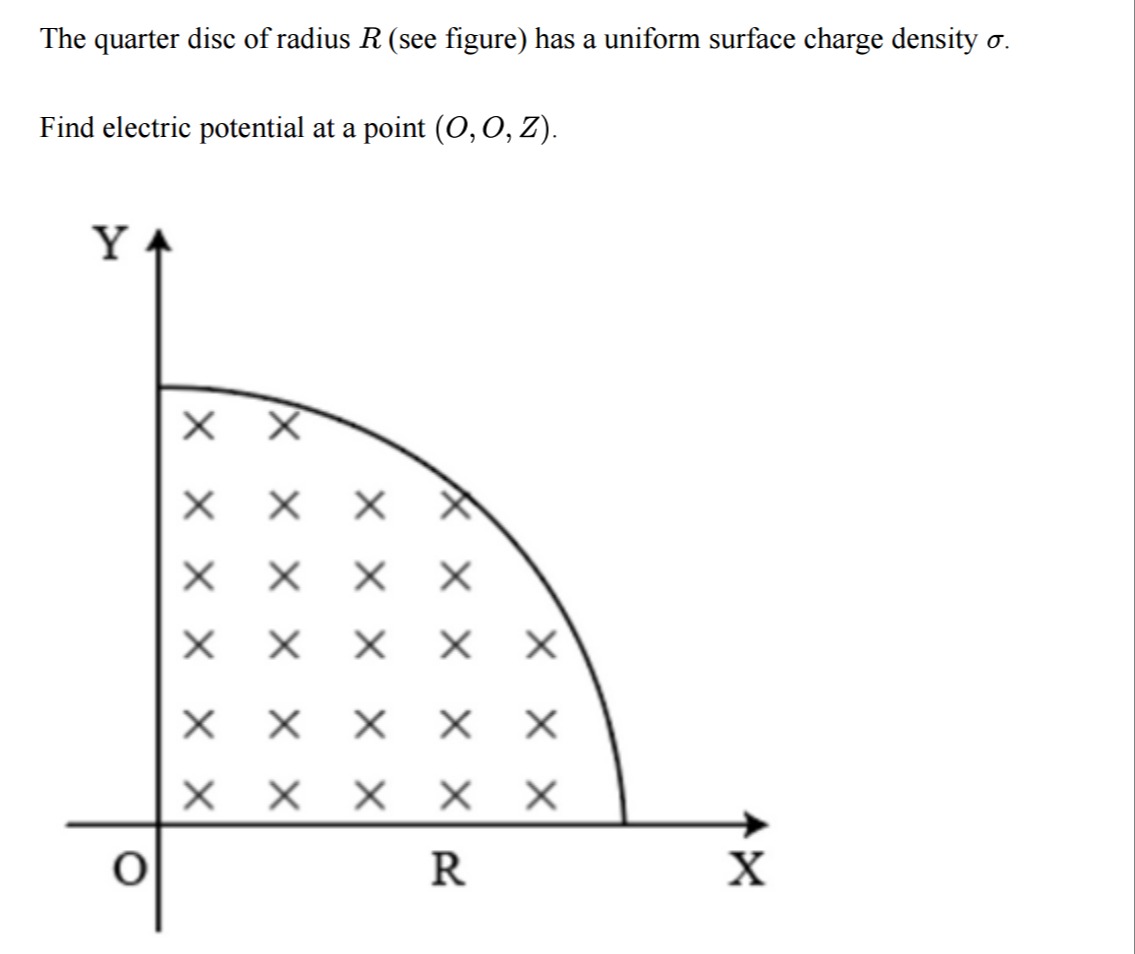
V = \frac{\sigma}{8\epsilon_0}\left(\sqrt{R^2+Z^2}-Z\right)

Answer 2

Step-by-step Solution

1. Set Up the Integral:

The quarter disc lies in the first quadrant of the $xy$-plane with uniform surface charge density $\sigma$. In polar coordinates, the disc is described by: $r \in [0, R], \quad \theta \in \left[0, \frac{\pi}{2}\right].$ An infinitesimal element of area is: $dA = r\,dr\,d\theta.$

2. Potential Contribution:

The potential at $(0,0,Z)$ due to an element of charge $dQ = \sigma dA$ is: $dV = \frac{1}{4\pi\epsilon_0} \frac{dQ}{\sqrt{r^2+Z^2}} = \frac{1}{4\pi\epsilon_0} \frac{\sigma\, r\,dr\,d\theta}{\sqrt{r^2+Z^2}}.$

3. Integrate Over the Quarter Disc:

   $$V = \frac{\sigma}{4\pi\epsilon_0} \int_0^{\frac{\pi}{2}} \int_0^R \frac{r}{\sqrt{r^2+Z^2}}\; dr\,d\theta.$$

   First, integrate over $\theta$:

   $$\int_0^{\frac{\pi}{2}} d\theta = \frac{\pi}{2}.$$

   Now, the potential becomes:

   $$V = \frac{\sigma}{4\pi\epsilon_0} \cdot \frac{\pi}{2} \int_0^R \frac{r}{\sqrt{r^2+Z^2}}\; dr.$$

4. Evaluate the Radial Integral:

   Let:

   $$I = \int_0^R \frac{r}{\sqrt{r^2+Z^2}}\; dr.$$

   Use the substitution:

   $$u = r^2 + Z^2 \quad \Rightarrow \quad du = 2r\,dr.$$

   Therefore:

   $$I = \frac{1}{2} \int_{Z^2}^{R^2+Z^2} u^{-1/2}\; du = \frac{1}{2} \cdot \left[ 2 u^{1/2} \right]_{Z^2}^{R^2+Z^2} = \sqrt{R^2+Z^2} - Z.$$

5. Final Expression:

   Substitute $I$ back:

   $$V = \frac{\sigma}{4\pi\epsilon_0} \cdot \frac{\pi}{2} \left(\sqrt{R^2+Z^2} - Z\right).$$

   Simplify:

   $$\frac{\pi}{4\pi} = \frac{1}{4} \quad \text{and} \quad \frac{1}{4} \cdot \frac{1}{2} = \frac{1}{8},$$

   so:

   $$V = \frac{\sigma}{8\epsilon_0}\left(\sqrt{R^2+Z^2}-Z\right).$$

---

Minimal Explanation of the Core Solution:

• Convert to polar coordinates.
• Write the potential $dV = \frac{1}{4\pi\epsilon_0} \frac{\sigma\, r\,dr\,d\theta}{\sqrt{r^2+Z^2}}$.
• Integrate over $\theta$ (factor $\pi/2$) and over $r$ using substitution $u = r^2+Z^2$.
• Final answer: $V = \frac{\sigma}{8\epsilon_0}\left(\sqrt{R^2+Z^2}-Z\right)$.