Question

The quantity jerk, J, is defined as the time derivative of an object's acceleration,
$J = \dfrac{{da}}{{dt}} = \dfrac{{{d^3}x}}{{d{t^3}}}$
What is the physical meaning of the area under a graph of jerk versus time.
A) The area represents the object's change in acceleration
B) The area represents the object's acceleration
C) The area represents the object's change in velocity
D) The area represents the object's velocity

Answer 1

When we are talking about an area under a curve, we are talking about performing integration operations on a curve, the integration can be performed with respect to either x-axis or y-axis. Consider the following figure for understanding his concept.

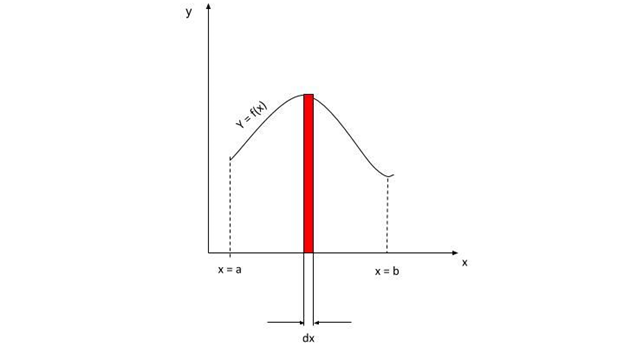
In the above figure the area under the entire curve can be found by calculating the area of the rectangle which is painted red and integrating it between the limits a to b. The area of the rectangle (dA) is equal to the product of height (y = f(x)) and width (dx).
$dA = ydx = f\left( x \right)dx$
$A = \int_a^b {f\left( x \right)dx}$

Complete step by step answer:

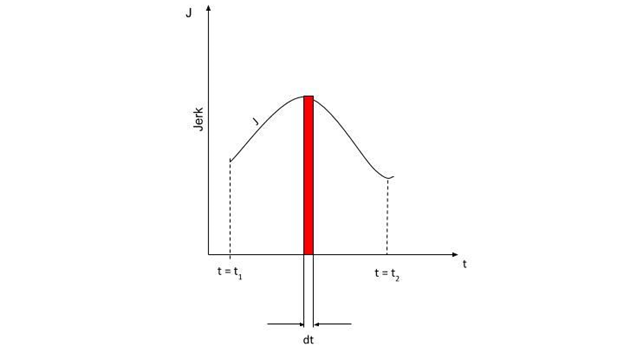
In the given question we have been provided with the definition of the quantity called jerk (J) as the time derivative of acceleration i.e.,
$J = \dfrac{{da}}{{dt}}$.......................(1)
Nw, the figure given above shows the graph of jerk vs. time. Hence, now the area (A) under the curve is given as,
$A = \int_{{t_1}}^{{t_2}} {Jdt}$
From equation (1), put the value of J in above equation
$A = \int_{{t_1}}^{{t_2}} {\dfrac{{da}}{{dt}}dt}$
$A = \int_{{t_1}}^{{t_2}} {da}$
$A = {a_{{t_2}}} - {a_{{t_1}}}$
Where, and are accelerations at time $t_1$ and $t_2$ respectively. So now we can say that,
$A = \Delta a$
i.e. area under the jerk vs. time curve is equal to the change in acceleration.

Note: One can easily get confused by applying the logic of integration and derivative, getting cancelled by each other as these operations are opposite in nature and say that the answer to this question will be acceleration and not the change in acceleration. However, it should be noticed that for definite integral the answer will be change in acceleration whereas for indefinite integral we will get acceleration as a function of time.