Question

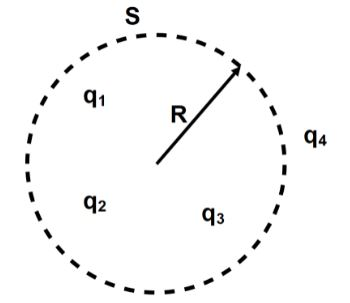
The $q_1,q_2,q_3$ and $q_4$ are point charges located at points as shown in the figure and $S$ is a spherical Gaussian surface of radius $R$. Which of the following is true according to Gauss's law?

A. $\oint\limits_{s}{\left( \overset{\to }{\mathop{{{E}_{1}}}}\,+\overset{\to }{\mathop{{{E}_{2}}}}\,+\overset{\to }{\mathop{{{E}_{3}}}}\, \right)}.\overset{\to }{\mathop{dA}}\,=\dfrac{\left( {{q}_{1}}+{{q}_{2}}+{{q}_{3}} \right)}{2{{\varepsilon }_{0}}}$
B. $\oint\limits_{s}{\left( \overset{\to }{\mathop{{{E}_{1}}}}\,+\overset{\to }{\mathop{{{E}_{2}}}}\,+\overset{\to }{\mathop{{{E}_{3}}}}\, \right)}.\overset{\to }{\mathop{dA}}\,=\dfrac{\left( {{q}_{1}}+{{q}_{2}}+{{q}_{3}} \right)}{{{\varepsilon }_{0}}}$
C. $\oint\limits_{s}{\left( \overset{\to }{\mathop{{{E}_{1}}}}\,+\overset{\to }{\mathop{{{E}_{2}}}}\,+\overset{\to }{\mathop{{{E}_{3}}}}\, \right)}.\overset{\to }{\mathop{dA}}\,=\dfrac{\left( {{q}_{1}}+{{q}_{2}}+{{q}_{3}}+{{q}_{4}} \right)}{{{\varepsilon }_{0}}}$
D. None of the above

Answer 1

We know that the Gauss law is applicable only for the charges that are included in the closed surface area, all the other charges that are outside the closed area are neglected. So, we will find the net charge inside the Gaussian surface and then find the net electric field using the Gaussian law by substituting the value of the magnitude of charge inside in the Gaussian formula.

Formula used:
Gauss’s law is given by,
$\oint\limits_{s}{\overset{\to }{\mathop{E}}\,}.\overset{\to }{\mathop{ds}}\,=\dfrac{{{q}_{enclosed}}}{{{\varepsilon }_{0}}}$
where $\overset{\to }{\mathop{E}}\,$ is the electric field, ds is a small area considered for all small amount of area it is given by $dA$, $q$ is charge within closed area and ${{\varepsilon }_{0}}$ is the permittivity due to free space.

Complete step by step answer:
As we know that the Gauss law states that the electric flux over a closed area is the charge enclosed in the closed area to that of the permittivity. The right side of the equation is the sum of the charge enclosed in a closed area. The Gauss law is applicable to only closed surfaces, this is because only closed surfaces possess all the electric field lines pointing in the same direction and these charges have the field lines that end up in zero.

This is not possible if charges are present in an open area. The given diagram shows the charges ${{q}_{2}}\And\, {{q}_{4}}$ only in closed areas. Hence these two alone are responsible for the electric flux in that area similarly the other charges ${{q}_{1}}\And \,{{q}_{3}}$ are not enclosed inside the closed surfaces. Hence these charges do not contribute to the electric flux over the area.

Thus, $\oint\limits_{s}{\overset{\to }{\mathop{E}}\,}.\overset{\to }{\mathop{ds}}\,=\dfrac{{{q}_{enclosed}}}{{{\varepsilon }_{0}}}$
Here we have given $q_1,q_2,q_3$ and $q_4$ are point charges located at points for S is a spherical Gaussian surface of radius R thus the $\overset{\to }{\mathop{E}}\,=\overset{\to }{\mathop{{{E}_{1}}}}\,+\overset{\to }{\mathop{{{E}_{2}}}}\,+\overset{\to }{\mathop{{{E}_{3}}}}\,$ and ${{q}_{enclosed}}={{q}_{1}}+{{q}_{2}}+{{q}_{3}}$ therefore, the equation can be by
$\therefore \oint\limits_{s}{\left( \overset{\to }{\mathop{{{E}_{1}}}}\,+\overset{\to }{\mathop{{{E}_{2}}}}\,+\overset{\to }{\mathop{{{E}_{3}}}}\, \right)}.\overset{\to }{\mathop{dA}}\,=\dfrac{\left( {{q}_{1}}+{{q}_{2}}+{{q}_{3}} \right)}{{{\varepsilon }_{0}}}$

Therefore, the correct answer is option B.

Note: If there is no charge in the gaussian surface, then according to the Gaussian law, the electric field will be zero. Also, if there are charges in the gaussian surface such that they cancel each other in magnitudes due to their opposite nature, the net electric field inside the Gaussian surface will be zero. Note that if we take a Gaussian surface inside a spherical shell, there will be no charge enclosed in it, so the electric field will be zero. This also explains the concept that the charges are spread uniformly over the outer surface of the shell.