Question
Question: The pulley shown in the figure has a moment of inertia \( I \) about its axis and its radius is \( r...
The pulley shown in the figure has a moment of inertia I about its axis and its radius is r . Calculate the magnitude of the acceleration of the two blocks. Assume that the string is light and does not slip on the pulley.
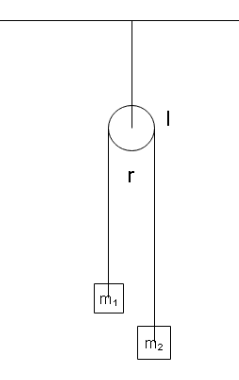
Solution
Assume that mass m2 is greater than m1 so m2 will fall on one side and m1 will rise on one side. The acceleration of the blocks can be calculated by balancing the linear acceleration associated with the angular motion of the rod with the accelerations of the blocks.
Formula used:
a=α×r where a is the linear acceleration associated with a rotated body of angular acceleration α and linear displacement r
Complete step by step solution:
We’ve been given that the string that connects the two blocks does not slip on the pulley. So whenever one mass falls and the other rises, the string moves the pulley along with it. Let us consider the linear acceleration due to the difference in mass of the blocks.
Since the string is under force, it will have tension in it. For the block of mass m1 that rises upwards with a net acceleration a , we can write the equation of motion as
m1g−T1=m1a
Similarly we can write the equation of the mass m2 that is moving downwards with a net acceleration a as:
T2−m2g=m2a
Now, the pulley will have the same angular acceleration as the string on it since the string does not slip on the pulley. The angular acceleration on the string can be equalized with the angular acceleration of the pulley as
T1r−T2r=Iα
Since a=α×r , we can write
T1r−T2r=rIa
Substituting the values of T1 and T2 from equation (1) and (2), we get
[(m1g−a)−m2(g+a)]r=rIa
Solving for a we can write
a=I+(m1+m2)r2(m1−m2)gr3 .
Note:
The tricky part in this question is realizing that the angular motion of the pulley is due to the motion of the string on it without slipping. In a real-world scenario, there is always some slippage of the string on the pulley as well as other friction forces that act between the string and the pulley.
