Question

The principal axis of an optical device is along $y = - 1$ , image of a small body placed $( - 30,3)$ is formed at a point $(60, - 3)$ . Then the optical device is:
(A) A convex lens of focal length $20cm$
(B) A concave mirror of focal length $60cm$
(C) A concave lens of focal length $20cm$
(D) A convex mirror of focal length $60cm$

Answer 1

Hint : Use the formula for the magnification to find the position of the device and use property of the image and then use the formula for lens or mirror to find the focal length of the device. Magnification of an object is given by, $m = \dfrac{{{h_i}}}{{{h_o}}} = \dfrac{v}{u}$ where, ${h_i}$ is the image height ${h_o}$ is the object height from the principal axis. Where, $v$ is the image distance and $u$ is the object distance. Len’s formula is given by, $\dfrac{1}{v} - \dfrac{1}{u} = \dfrac{1}{f}$ where $f$ is the focal length. Mirror’s formula is given by, $\dfrac{1}{v} + \dfrac{1}{u} = \dfrac{1}{f}$

Complete Step By Step Answer:
We know the magnification of an object is given by, $m = \dfrac{{{h_i}}}{{{h_o}}} = \dfrac{v}{u}$ where, ${h_i}$ is the image height ${h_o}$ is the object height from the principal axis.
Here, we have given that the image is at $(60, - 3)$ , the object is at $( - 30,3)$ . The principal axis of the optical device is along $y = - 1$ . Hence, height of the object will be the distance of the object from the $y = - 1$ axis.
That becomes, ${h_o} = 3 - ( - 1) = 4cm$ and height of the image is , ${h_i} = - 3 - ( - 1) = - 2cm$ . Negative sign implies that the image is inverted.
Hence, we can find the magnification. Magnification, $m = \dfrac{{{h_i}}}{{{h_o}}}$
Putting the values we get,
$m = \dfrac{{ - 2}}{4} = - \dfrac{1}{2}$ .
Hence, the ratio of the image to object distance will be also the same.
$\dfrac{v}{u} = - \dfrac{1}{2}$ .

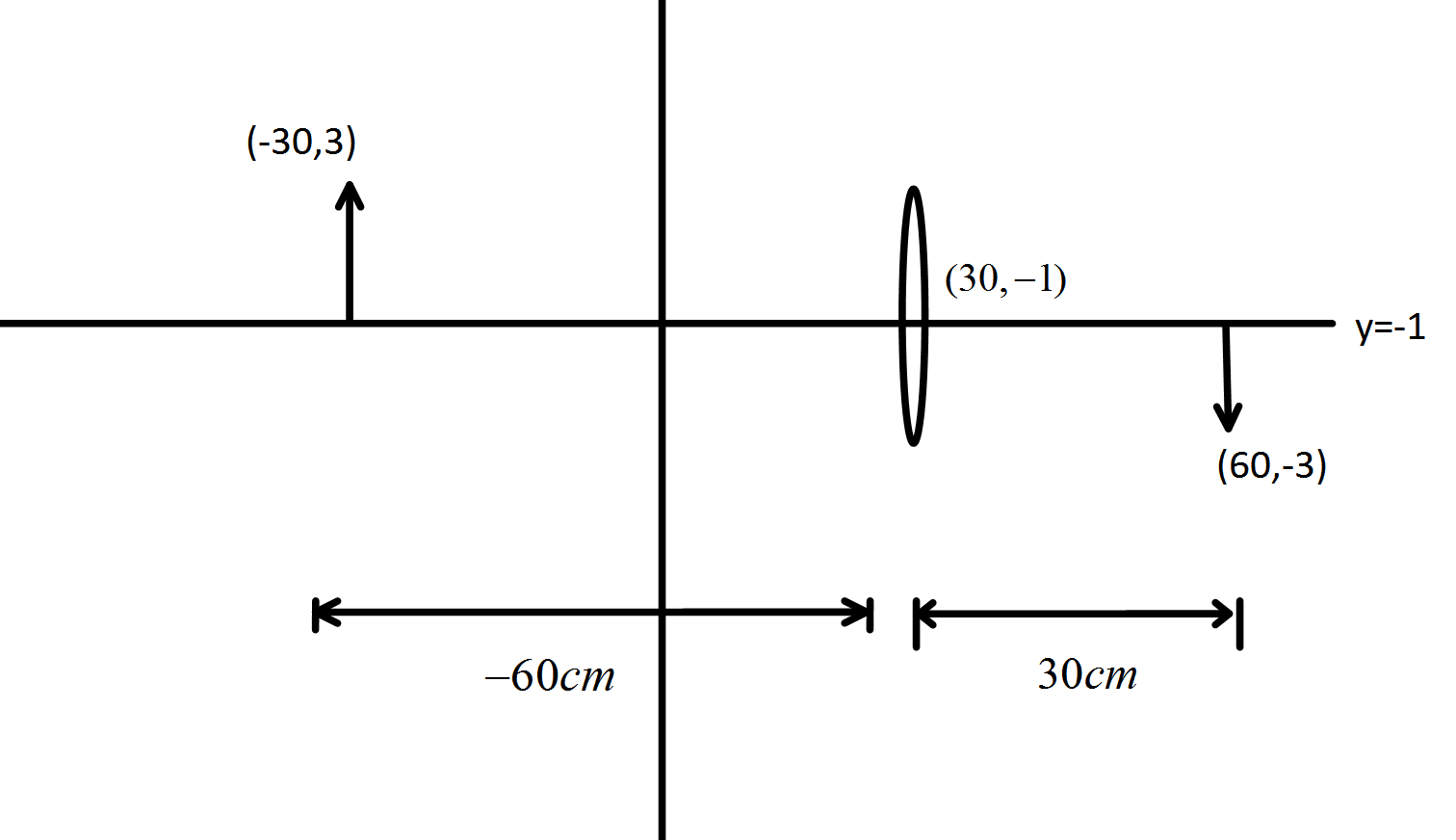
Now, we have to find the position of the optical device, let, the device is at a distance of $xcm$ from the object, hence, new object distance will be $- xcm$ and the image distance will be, $(90 - x)cm$ . Since, the distance between the image and object is $90cm$ . So, we can write,
$\dfrac{{(90 - x)}}{{ - x}} = - \dfrac{1}{2}$
$\Rightarrow 2x - 180 = - x$
$\Rightarrow 3x = 180$
Hence,
$x = 60$
Hence, the optical device is at a distance of $60cm$ from the object. Hence coordinate of it is,
$( - 30 + 60, - 1) = (30, - 1)$
Hence, image distance from the device will be, $v = 60 - 30 = 30cm$ and object distance will be, $u = - 30 - 30 = - 60cm$
Now, to find the focal length of the device we have to use the formula for lens and mirror.
We know, len’s formula is given by, $\dfrac{1}{v} - \dfrac{1}{u} = \dfrac{1}{f}$ where $f$ is the focal length.
Putting the values we get,
$\dfrac{1}{{30}} - \dfrac{1}{{ - 60}} = \dfrac{1}{f}$
Or, $\dfrac{{2 + 1}}{{60}} = \dfrac{1}{f}$
Or, $f = 20cm$ .
Since, focal length of the device is positive hence it is a convex lens of focal length $20cm$ .
Now we know, mirror’s formula is given by, $\dfrac{1}{v} + \dfrac{1}{u} = \dfrac{1}{f}$ where $f$ is the focal length.
Putting the values we get,
$\dfrac{1}{{30}} + \dfrac{1}{{ - 60}} = \dfrac{1}{f}$
Or, $\dfrac{{2 - 1}}{{60}} = \dfrac{1}{f}$
Or, $f = 60cm$ .
Since, the focal length of the device is positive hence it is a convex mirror of focal length $60cm$ .
But, we know the image formed by a convex mirror is always erect. But here we have, inverted image. Hence, the device cannot be a convex mirror.
Hence, it is a convex lens of focal length of $20cm$ .
Hence, option (A) is correct.

Note :
Focal length of an optical device is the length of a point on the principal axis from the lens where parallel rays of light meet. For a convex mirror it is positive and for a concave mirror it is negative. On the contrary, for a convex lens it is positive and for a concave lens it is negative.