Question
Question: The pressure $P(z)$ as the function of $z$ is...
The pressure P(z) as the function of z is
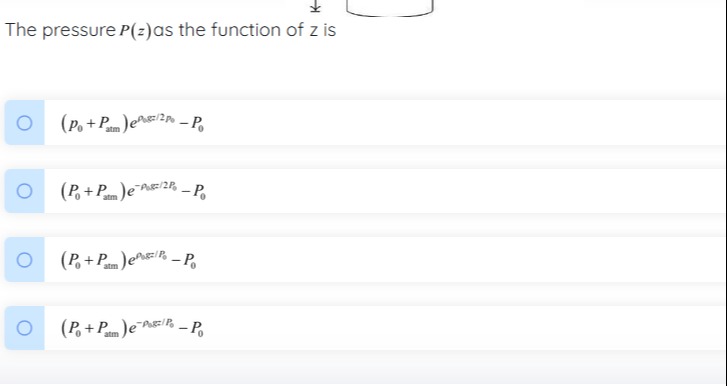
(p0+Patm)eρ0gz/2P0−P0
(P0+Patm)e−ρ0gz/2P0−P0
(P0+Patm)eρ0gz/P0−P0
(P0+Patm)e−ρ0gz/P0−P0
(P_0 + P_{atm})e^{-\rho_0 gz/P_0} - P_0
Solution
The pressure variation with height z is given by dP=−ρgdz. Assuming a linear relationship between density ρ and pressure P of the form ρ=aP+b, the integration of the differential equation leads to a pressure function of the form P(z)=Ae−agz−b/a. Comparing this with the given options, specifically option 4, P(z)=(P0+Patm)e−ρ0gz/P0−P0, we can identify b/a=P0, ag=ρ0g/P0, and A=P0+Patm. From b/a=P0, we get b=aP0. The density relation becomes ρ=aP+aP0=a(P+P0). From ag=ρ0g/P0, we get a=ρ0/P0. Substituting a=ρ0/P0 into the density relation gives ρ=(ρ0/P0)(P+P0)=(ρ0/P0)P+ρ0. The term A=P0+Patm is consistent with the boundary condition P(0)=Patm, as A=a1(aP(0)+b)=P(0)+b/a=P(0)+P0, which implies P(0)=Patm. This shows that option 4 is derived from the differential equation dP=−ρgdz with the density-pressure relationship ρ=(ρ0/P0)P+ρ0 and the boundary condition P(0)=Patm.
